Question

Нужна помощь с данным заданием) Буду признателен, если кто-то реально поможет)

Answer 1

Пусть высота пирамиды проходит через вершину А основания.

Поэтому одно боковое ребро совпадает с высотой пирамиды.

Боковая поверхность пирамиды состоит из трёх пар равных граней.

Назовём их 1 и 6, 2 и 5, 3 и 4.

S(1; 6) = (1/2)a².

У граней 2 и 5 высота равна √(a² + (a√3/2)²) = √(a² + 3a²/4) = a√7/2.

S(2; 5) = (1/2)a*(a√7/2) = a²√7/4.

У граней 3 и 4 одно наклонное ребро равно:

√(a² + (a√3)²) = √(a² + 3a²) = 2a.

Оно составляет прямой угол с ребром основания.

S(3; 4) = (1/2)a*2a = a².

Теперь можно определить сумму площадей боковых граней.

Sбок = 2(((1/2)a²) + (a²√7/4) + a²) = 2(6a² + (a²√7))/4 = (6a² + (a²√7))/2.

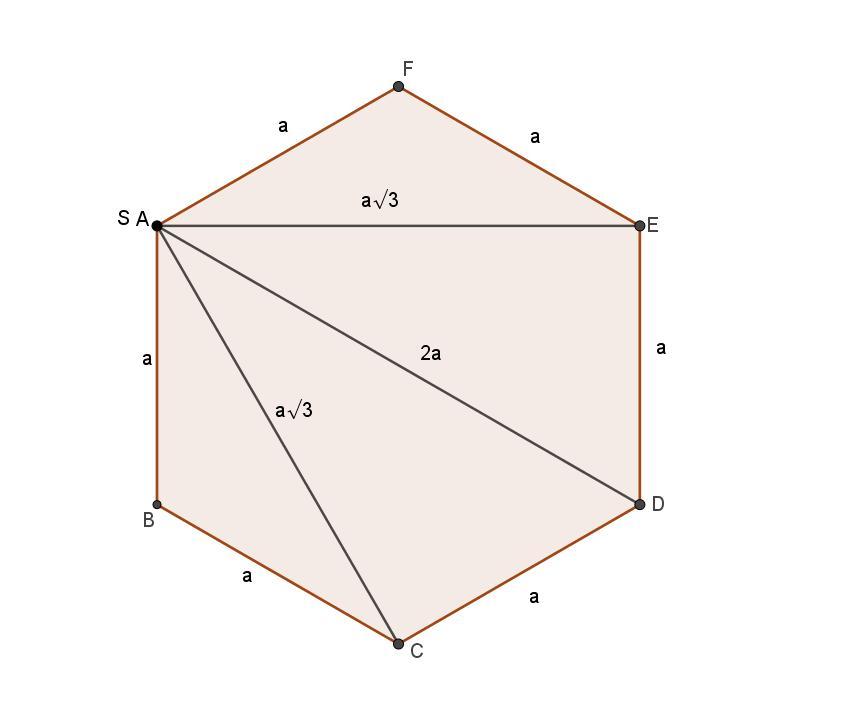
Во вложении дан план пирамиды (горизонтальная проекция).