Предмет: Алгебра,
автор: nikitkashadrin
ПОМОГИТЕ РЕШИТЬ УРАВНЕНИЕ УМОЛЯЮ
Приложения:
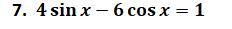
Ответы
Автор ответа:
2
Объяснение:
Разложи синус и косинус как двойной угол, а единицу распиши:
4sinx - 6cosx = 1
8sin(x/2)cos(x/2) - 6cos^2(x/2)+6sin^2(x/2) = sin^2(x/2)+cos^2(x/2)
Переносим в одну часть:
8sin(x/2)cos(x/2) - 7cos^2(x/2) + 5sin^2(x/2) = 0
Теперь дели либо на синус, либо на косинус:
8sin(x/2)cos(x/2) - 7cos^2(x/2) + 5sin^2(x/2) = 0 / cos^2(x/2)
8tg(x/2) - 7 + 5tg^2(x/2) = 0
делаешь замену - tg(x/2)=t
8t - 7 + 5t^2 = 0
5t^2 + 8t - 7 = 0
t1,2=((-8)+-корень(64-4*8*(-7)))/(2*8). Корни: -2,23 и 0,62 (перепроверь!!!)
Если tg(x/2)=t, то tg(x/2)=-2.23 и tg(x/2)=0.62
Cледовательно, (x/2)=-arctg(2.23)+2pi*k ; (x/2)=arctg(0.62)+2pi*k
x1=-2arctg(2.23)+4pi*k ; x2=2arctg(0.62)+4pi*k, k - целое
Не забудь написать, что cos(x)<>0!
nikitkashadrin:
спасибо что скопировал и вставил но мне бы нормальное решение а не это
Похожие вопросы
Предмет: Українська мова,
автор: s24bsa1
Предмет: Русский язык,
автор: rfgthjuyt6
Предмет: Русский язык,
автор: тима168
Предмет: Английский язык,
автор: DimaZagumenkin
Предмет: Физика,
автор: ElderSteve