Предмет: Геометрия,
автор: erinmoore1998
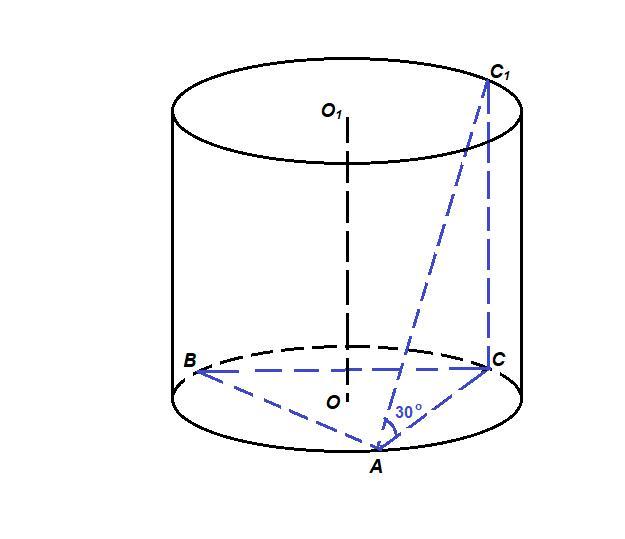
На окружности одного основания цилиндра выбраны точки A, B и C, на окружности другого основания - точка C1, CC1 - образующая цилиндра, а отрезок AC1 не пересекает ось цилиндра и образует с плоскостью основания цилиндра угол 30 градусов. Найдите объем цилиндра, если AB=AC=6 , угол BAC=60 градусов.
, угол BAC=60 градусов.
Ответы
Автор ответа:
1
Ответ:
216π куб. ед.
Объяснение:
АВ = АС, ΔАВС - равнобедренный,
∠ВАС = 60°, значит треугольник равносторонний.
Радиус описанной окружности около равностороннего треугольника:
где а - сторона треугольника.
Из прямоугольного треугольника АСС₁:
Объем цилиндра:
Приложения:
Похожие вопросы
Предмет: Английский язык,
автор: мужской3
Предмет: Русский язык,
автор: Аноним
Предмет: Окружающий мир,
автор: Аноним
Предмет: Литература,
автор: RaINbOWdAS