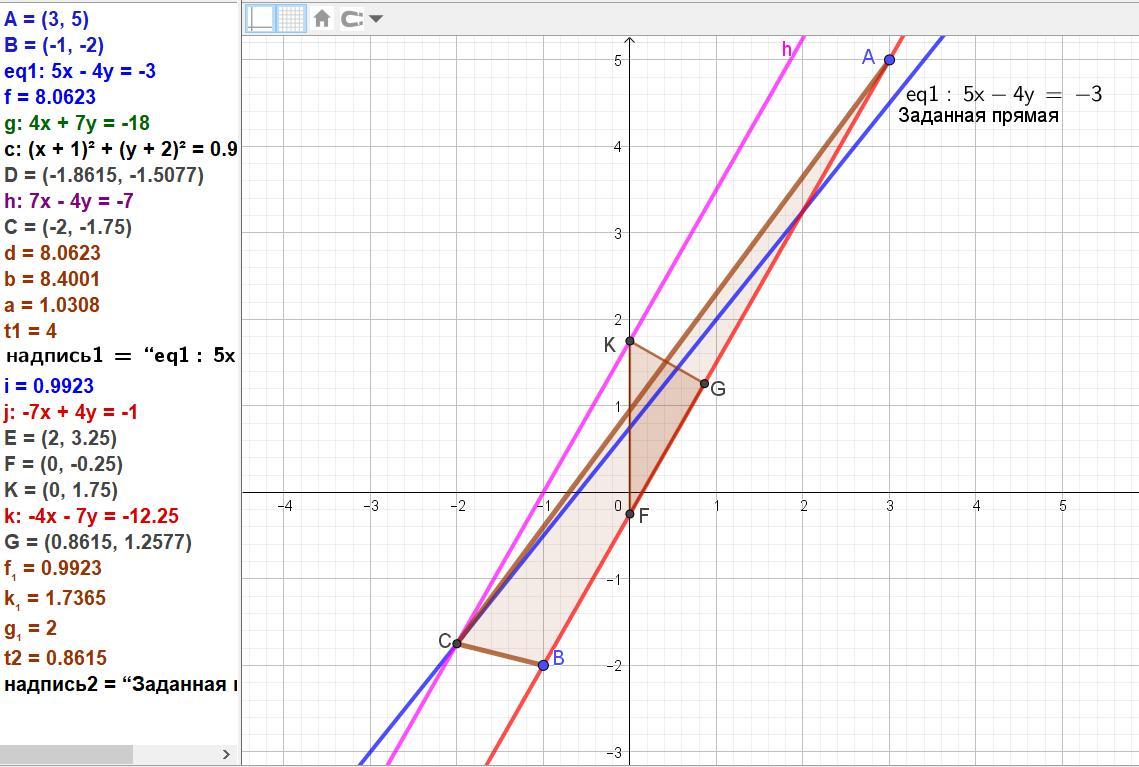
Две вершины треугольника находятся в точках А(3,5) и В(-1,-2), а третья вершина С находятся на прямой 5х-4у+3=0. Чему равна точка С, если площадь треугольника АВС равна 4.
Ответы
Две вершины треугольника находятся в точках А(3; 5) и В(-1; -2), а третья вершина С находятся на прямой 5х-4у+3=0. Чему равна точка С, если площадь треугольника АВС равна 4.
Вектор ВА равен (3-(-1); 5-(-2))= (4; 7).
Длина отрезка ВА равна:
|ВА| = √(4^2+7^2 )=√(16+49)=√65.
Уравнение прямой ВА равно:
(x + 1)/4 = (y + 2)/7.
7x + 7 = 4y + 8 и получаем общее уравнение прямой ВА:
7x – 4y – 1 = 0.
Высота h треугольника АВС на сторону АВ равна:
h = 2S/|ВА| = 2*4/√65=8/√65.
Уравнение прямой ВА с угловым коэффициентом:
y = (7/4)x – (1/4).
Величина –(1/4) это координата точки F пересечения прямой ВА оси Оу.
Найдём значение коэффициента b в уравнении прямой вида у = ах + b, параллельной ВА на расстоянии, равном h = 8/√65.
Тангенс угла наклона прямой ВА к оси Ох равен tg α = Δy/Δx = 7/4.
Косинус этого угла определим по формуле:
cos α = 1/√(1+tg² α) = 1/√(1+(49/16)) = 4/√65.
Тогда вертикальное расстояние FK между параллельными прямыми равно:
FK = h/cos α = (8/√65)/(4/√65)=2.
Координата точки К пересечения параллельной прямой с осью Оу равна (-1/4) + 2 = 7/4.
Точка К(0; (7/4)).
Найдем уравнение прямой CK, проходящей через точку K(0; (7/4)), параллельно прямой y = (7/4)x –(1/4).
Уравнение CK параллельно AB находится по формуле:
y - y0 = k(x - x0)
Подставляя x0 = 0, k = 7/4, y0 = 7/4, получим:
y-(7/4) = (7/4)(x-0)
или
y = (7/4)x + (7/4) или 7x – 4y + 7 = 0.
Координаты точки С найдём как точки пересечения заданной прямой 5х – 4у + 3 = 0 и прямой 7x – 4y + 7 = 0, проходящей параллельно АВ на расстоянии от неё h = 8/√65.
5х – 4у + 3 = 0
7x – 4y + 7 = 0, вычтем из второго уравнения первое:
2х + 4 = 0, отсюда х = -4/2 = -2.
Значение у найдём, подставив х = -2 в уравнение прямой.
5*(-2) – 4у + 3 = 0, 4у = -10 + 3 = -7, у = -7/4.
Ответ: точка С(-2; (-7/4).