Предмет: Математика,
автор: srarddd
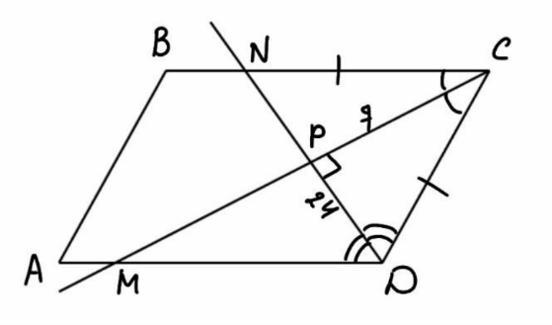
23. Биссектрисы углов при стороне CD параллелограмма ABCD пересе-
каются в точке Р. Найдите CD, если CP = 7, DP = 24.
помогитееее
Ответы
Автор ответа:
11
Биссектриса угла параллелограмма отсекает от него равнобедренный треугольник.
△CND — равнобедренный с основанием ND.
Так как биссектриса ∠DCN проведена к основанию равнобедренного треугольника, то она является еще и высотой.
Значит, CP ⊥ ND и ∠CPD = 90°.
Рассмотрим прямоугольный △ CPD.
По теореме Пифагора, CD² = CP² + DP².
Отсюда,
Ответ: CD = 25.
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: garaga2145422
Предмет: Русский язык,
автор: tanyacherenkova
Предмет: Русский язык,
автор: rozahoang
Предмет: Алгебра,
автор: Kadilya
Предмет: Русский язык,
автор: ikramjan