Question

вычислите острый угол между диагоналями куба

Answer 1

Ответ:

$arccos \dfrac{1}{3}$

Пошаговое объяснение:

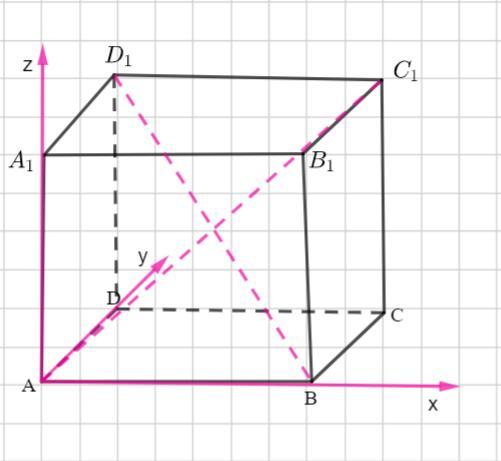
Введем систему координат и решим данную задачу методом координат.

Пусть ребро куба равно 1.

Рассмотрим диагонали куба $AC_{1}$ и  $BD_{1}$.

Найдем координаты данных точек

$A(0;0;0) ; C _{1} (1;1;1) ;\\B(1;0;0) ; D_{1} (0;1;1)$

Рассмотрим направляющие векторы прямых диагоналей .

Найдем координаты векторов. Для этого от координат конца вектора  надо отнять соответствующую координату начала вектора.

$\vec{AC_{1} }(1;1;1);\\\vec{BD_{1} }(-1;1;1)$

Воспользуемся скалярным произведением векторов и найдем косинус угла между векторами.

$\vec{AC_{1} }\cdot\vec{BD_{1} }=|\vec{AC_{1} }|\cdot |\vec{BD_{1} }|\cdot cos\alpha,$

где $\alpha -$ угол между векторами.

$cos \alpha =\dfrac{|\vec{AC_{1}\cdot \vec{BD_{1} |} }}{|\vec{AC_{1} }|\cdot |\vec{BD_{1} |}} \\\\cos \alpha =\dfrac{|1\cdot(-1)+1\cdot1+1\cdot1|}{\sqrt{(-1)^{2} +1^{2} +1^{2} } \cdot\sqrt{1^{2} +1^{2}+1^{2} } } =\dfrac{|-1+1+1|}{\sqrt{3} \cdot \sqrt{3} } =\dfrac{1}{3}$

$\alpha =arccos \dfrac{1}{3}$