Предмет: Геометрия,
автор: alena5566d
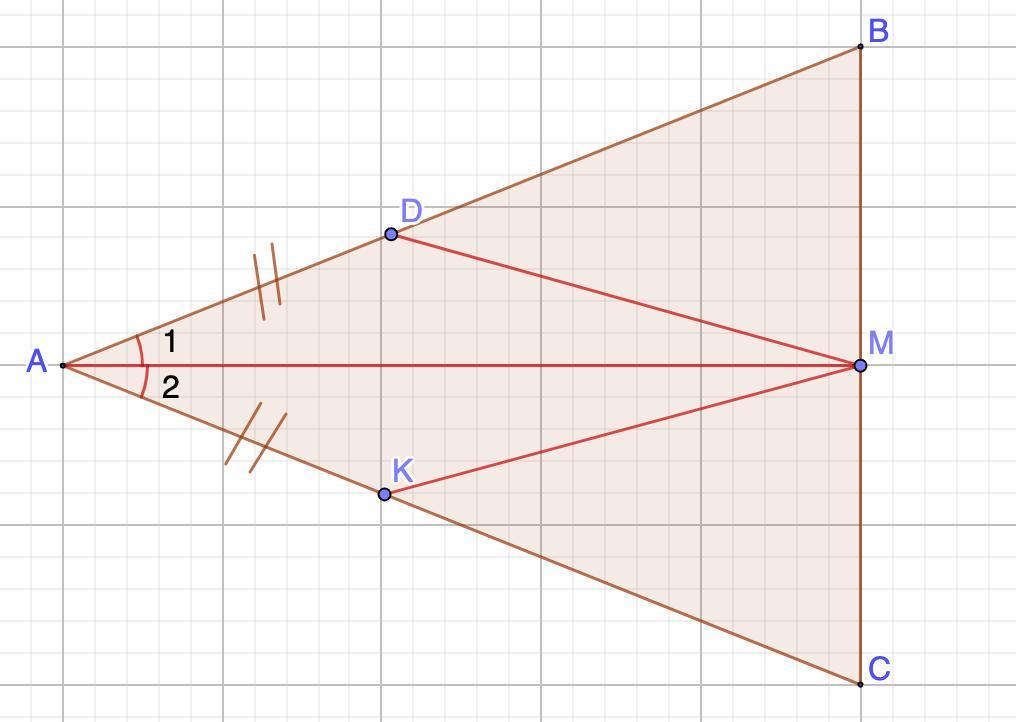
Дан равнобедренный треугольник АВС с основанием ВС. На боковых сторонах отмечены точки D и К так, что АD=АК. Из вершины А проведена биссектриса угла АМ. Доказать, что DМ=МК.
СРОЧНО, ПОЖАЛУЙСТА с чертежом!!!
ДАЮ 100 БАЛЛОВ!!!!!!!!
Ответы
Автор ответа:
1
Объяснение:
Дано: Δ АВС - равнобедренный.
АD=АК;
АМ - биссектриса
Доказать: DМ=МК
Доказательство:
Рассмотрим ΔАDМ и ΔАМК
∠1 = ∠2 (АМ - биссектриса)
АD=АК (условие)
АМ - общая
⇒ ΔАDМ = ΔАМ (по двум сторонам и углу между ними. 1 признак)
DМ=МК (как соответственные элементы)
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: полина785
Предмет: Русский язык,
автор: petr17
Предмет: Русский язык,
автор: ivan092
Предмет: Химия,
автор: Книголюбитель
Предмет: Математика,
автор: gloomynknight174