Предмет: Математика,
автор: StRiHoK
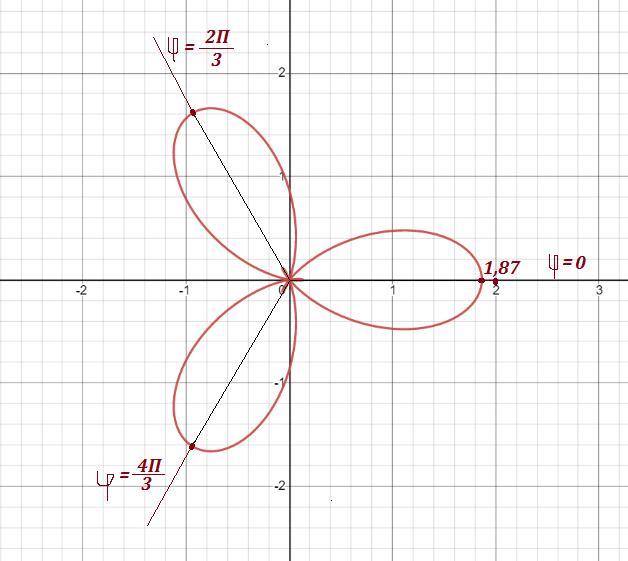
Построить график функции в полярной системе координат.
ρ= 
ПОМОГИТЕ ПОЖАЛУЙСТА.
100 БАЛЛОВ.
Ответы
Автор ответа:
0
Ответ:
Придаём значения и вычисляем
.
Приложения:
Похожие вопросы
Предмет: Английский язык,
автор: karina1488o
Предмет: Русский язык,
автор: daniniil
Предмет: Английский язык,
автор: ksyuxabomba03
Предмет: Алгебра,
автор: nikolya666
Предмет: Информатика,
автор: abduganievraximjon