СРОЧНО ПОМОГИТЕ!!! ДАЮ 35 БАЛЛОВ!
Решить нужно методом Гаусса.
(Желательно все расписать)
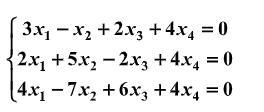
Ответы
Ответ:
, где
и
свободные переменные.
Пошаговое объяснение:
Запишем расширенную матрицу системы и с помощью элементарных преобразований приведем ее к ступенчатому виду.
Вторую строку матрицы умножим на (-2) и прибавим ее к третьей строке.
Первую строку матрицы умножим на и прибавим ее ко второй строке.
Вторую строку матрицы умножим на 3 и прибавим ее к третьей строке.
Строку, состоящую из одних нулей откидываем. Матрица приобретает вид:
Во второй строке больше невозможно дополнительно ни один элемент сделать нулевым.
Система уравнений теперь имеет вид:
Значит система уравнений имеет бесконечно много решений.
и
- базисные переменные (базисные переменные всегда находятся на ступенях матрицы).
и
- свободные переменные. Через них выразим базисные переменные.
Из второго уравнения системы выражаем .
Подставляем в первое уравнение системы и выражаем
.
Ответ:
, где
и
свободные переменные.
Проверка общего решения. Для этого общее решение подставляем в каждое уравнение исходной системы и производим вычисления.