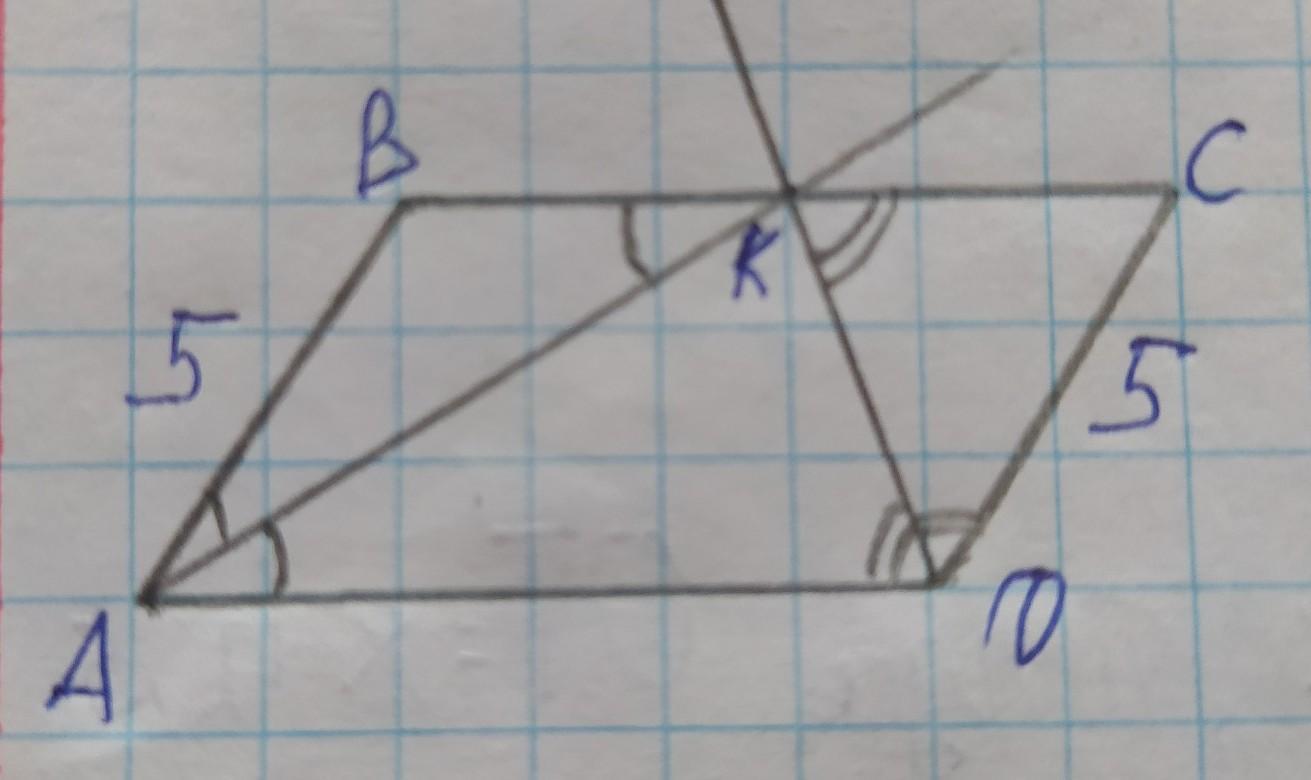
Найдите периметр параллелограмма ABCD, если его меньшая сторона равна 5 см, а биссектрисы углов A и D пересекаются в точке K, лежащей на стороне BC. Найдите меру угла AKD. ( с объяснением и с рисунком пж.)
Ответы
Сума углов BAD и CDA = 180° (свойство параллелограмма)
Углы BAK с KAD и углы KDA с KDC равны (так как AK и DK - биссектрисы этих углов соответственно)
Значит сума углов BAK, KAD, KDA, KDC = 180°
Пусть углы BAK и KAD - a, углы KDA и KDC- b
Тогда 2a + 2b= 180°
a + b = 90°
Поскольку сума углов треугольника 180°, а сума углов KAD и KDA = 90°, то угол AKD = 90°
AK - секущая прямая двух параллельных прямых BC и AD
Тогда углы BKA и KAD равны
А так как углы BAK и KAD равны то треугольник BAK - равнобедренный с основой AK
Тогда AB = BK = 5см
KD - секущая прямая двух параллельных прямых BC и AD
Тогда углы KDA и CKD равны
А так как углы CDK и KDC равны то треугольник CDK - равнобедренный с основой KD
Тогда CK = CD = 5см
BC = AD = CK + BK = 5 + 5 = 10(см)
P = 2(AB + BC) = 2(5 + 10) = 30(см)
Ответ: P = 30 см; угол AKD = 90°