Замените М таким многочленом , чтоб полученное равенство было тождеством : а) М+(x²-y)=2x²+3y-1
б) М-(b²+3bc)=2b²+c
в) (a²-ab+b²)-M=2a²+2b²
СРОЧНОО ПОЖАЛУЙСТА!!!!!
Ответы
Ответ:
на фото
Объяснение:
....................
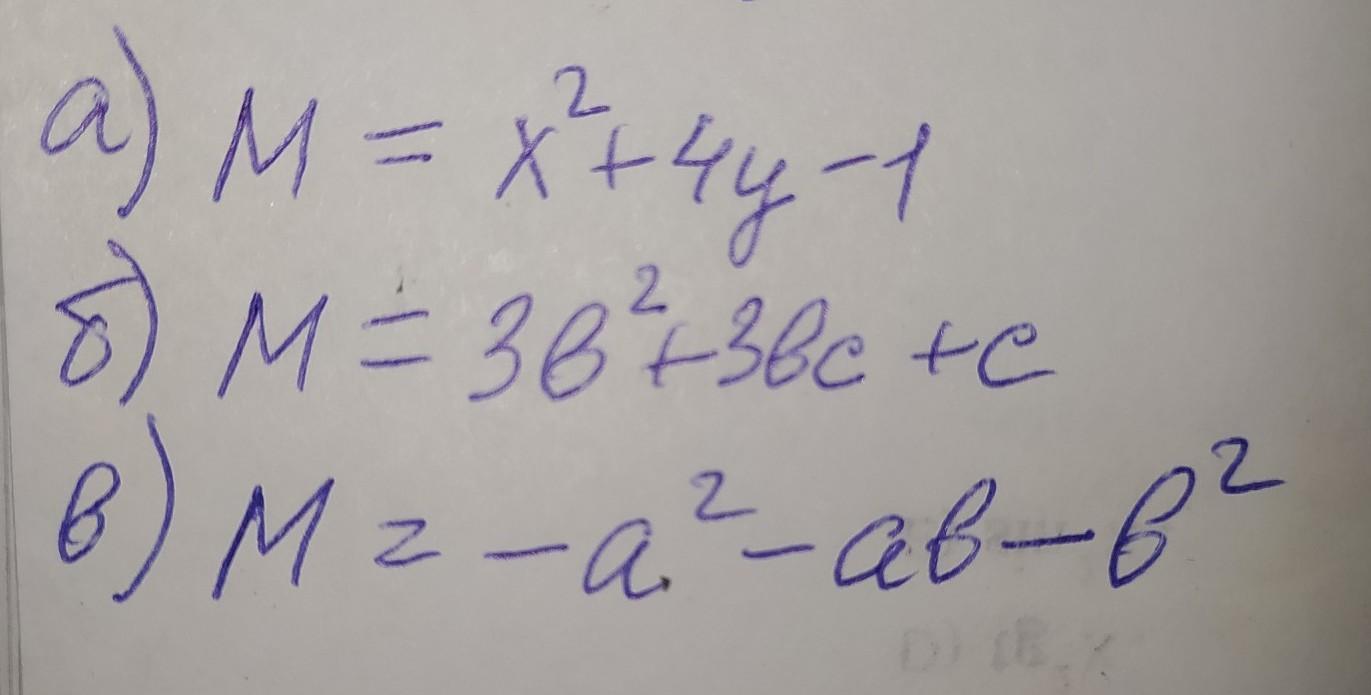
Ответ:
В решении.
Объяснение:
Памятка:
Как найти сумму и разность многочленов и записать результат как многочлен стандартного вида.
1) Записать многочлены в одну строку, второй многочлен в скобках, между ними знак + или -.
2) Раскрыть скобки. Если между многочленами знак +, во втором многочлене знаки не меняются, если перед скобками знак -, меняются на противоположные.
3) Привести подобные члены.
4) Записать результат в стандартном виде, т.е., в порядке убывания степеней и в алфавитном порядке.
Замените М таким многочленом , чтоб полученное равенство было тождеством:
а) М + (x² - y) = 2x² + 3y - 1
М = (2x² + 3y - 1) - (x² - y)
М = 2x² + 3y - 1 - x² + y
М = х² + 4у -1.
Проверка:
х² + 4у -1 + х² - у = 2х² + 3у - 1.
б) М - (b² + 3bc) = 2b² + c
М = (2b² + c) + (b² + 3bc)
М = 2b² + c + b² + 3bc
M = 3b² + 3bc + c.
Проверка:
3b² + 3bc + c - (b² + 3bc) = 3b² + 3bc + c - b² - 3bc = 2b² + c.
в) (a² - ab + b²) - M = 2a² + 2b²
М = (a² - ab + b²) - (2a² + 2b²)
М = a² - ab + b² - 2a² - 2b²
М = -а² - ab - b².
Проверка:
(a² - ab + b²) - (-а² - ab - b²) = a² - ab + b² + а² + ab + b² = 2a² + 2b².