Предмет: Математика,
автор: like167
Найти все целые n, при которых справедливо равенство
Приложения:
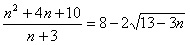
Ответы
Автор ответа:
0
Чтобы это уравнение имело целое решение, 13 - 3n должно быть квадратом.
13 - 3n >= 0, 3n <= 13, n <= 13/3, целое n <= 4
При n = 4 получаем
(16 + 16 + 10)/7 = 8 - 2√(13-12)
42/7 = 8 - 2*1 - верно.
При n = 3 получаем
(9 + 12 + 10)/6 = 8 - 2√(13-9)
31/6 = 8 - 2*2 - не верно.
При n = 0, 1, 2 под корнем будет не квадрат.
При n = -1 получаем
(1 - 4 + 10)/2 = 8 - 2√(13+3)
7/2 = 8 - 2*4 - не верно
При n = -2, -3 под корнем будет не квадрат
При n = -4 получаем
(16-16+10)/(-1) = 8 - 2*√(13+12)
-10 = 8 - 2*5 - не верно
Дальше корней не будет, потому что левая часть уменьшается намного быстрее правой. И тем более целых корней.
Поэтому единственный целый корень n = 4.
Кроме того, Нигма показывает, что это вообще единственный вещественный корень.
13 - 3n >= 0, 3n <= 13, n <= 13/3, целое n <= 4
При n = 4 получаем
(16 + 16 + 10)/7 = 8 - 2√(13-12)
42/7 = 8 - 2*1 - верно.
При n = 3 получаем
(9 + 12 + 10)/6 = 8 - 2√(13-9)
31/6 = 8 - 2*2 - не верно.
При n = 0, 1, 2 под корнем будет не квадрат.
При n = -1 получаем
(1 - 4 + 10)/2 = 8 - 2√(13+3)
7/2 = 8 - 2*4 - не верно
При n = -2, -3 под корнем будет не квадрат
При n = -4 получаем
(16-16+10)/(-1) = 8 - 2*√(13+12)
-10 = 8 - 2*5 - не верно
Дальше корней не будет, потому что левая часть уменьшается намного быстрее правой. И тем более целых корней.
Поэтому единственный целый корень n = 4.
Кроме того, Нигма показывает, что это вообще единственный вещественный корень.
Похожие вопросы
Предмет: Информатика,
автор: hjdgjejrj
Предмет: Қазақ тiлi,
автор: romangunhcevskij
Предмет: Английский язык,
автор: znaika0004
Предмет: Математика,
автор: RitaStewart16