Question

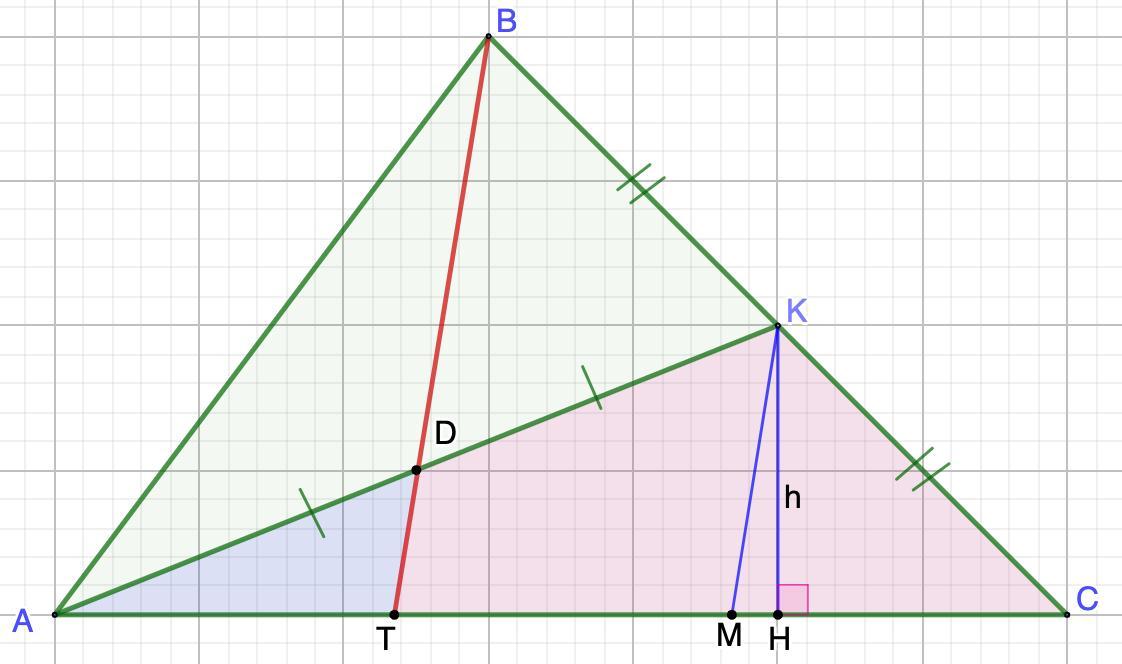
Через середину D медианы АК треугольника ABC и вершину проведена прямая, пересекающая сторону AC в точке Т. Найдите отношение площади треугольника ADT к площади четырёхугольника CKDT.​

Answer 1

Ответ:

1/5

Объяснение:

Проведем КР параллельно ВТ , так, что  Р лежит на ТС.

Понятно, что АТ=ТР, т.к. DT средняя линия в АКР. Также ТР=РС, т.к. КР - средняя линия в ВТС. Значит АТ=АС/3.

Пусть S - площадь АВС.

Площадь АВК=S/2 (медиана делит на равновеликие треугольники)

Площадь АDВ=S/4

Площадь АВТ=S/3 (основание АС втрое больше АТ, а высоты ВАТ и АВС к АС равны).

Значит площадь АDТ=S(1/3-1/4)=S/12

Площадь КDТС=(S/2)-S/12=5*S/12

Искомое отношение (S/12):(5*S/12)=1/5

Answer 2

Объяснение:

Дано: ΔАВС;

АК - медиана;

AD=DK.

Найти: ΔADT : CKDT

Решение:

Проведем КМ || ВТ.

Проведем высоту h.

1. Рассмотрим ΔАКМ.

AD=DK (условие)

ТD || КМ (построение)

• Если отрезок в треугольнике проходит через середину одной из его сторон, пересекает вторую и параллелен третьей — этот отрезок можно назвать средней линией этого треугольника.

⇒ TD - средняя линия ΔАКМ.

⇒ АТ=ТМ

2. Рассмотрим Δ ТВС.

ВК=КС (АК - медиана)

КМ || ВТ (построение)

⇒ МК - средняя линия ΔТВС

⇒ ТМ=МС

Из пунктов 1 и 2 следует

АТ=ТМ=МС.

3. Пусть АТ=ТМ=МС=а

• Площадь треугольника равна половине произведения основания на высоту.

$\displaystyle S_{AKC}=\frac{1}{2}AC*h=\frac{3ah}{2}$

$\displaystyle S_{AKM}=\frac{1}{2}AM*h=\frac{2ah}{2}=ah$

• Средняя линия отсекает треугольник, площадь которого равна одной четвёртой площади исходного треугольника.

⇒

$\displaystyle S_{ADT}=\frac{1}{4}S_{AKM}=\frac{1}{4}*ah =\frac{ah}{4}$

$\displaystyle S_{CKDT}=S_{AKC}-S_{ADT}=\frac{3ah}{2}-\frac{ah}{4}=\frac{5ah}{4}$

$\displaystyle \frac{S_{ADT}}{S_{CKDT}}=\frac{ah*4}{4*5ah} }=\frac{1}{5}$