Предмет: Математика,
автор: worldmen
Знайти інтеграли, використовуючи метод інтегрування частинами.
Приложения:
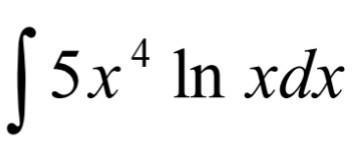
Ответы
Автор ответа:
1
Привет)
=
worldmen:
После знака = начинается непрогруженный пример.
я там сместил ниже
багуется что ли
походу
Не мог бы ты переписать или изменить?
сейчас
"Ошибка в формуле. Попробуйте ее исправить или разделить на несколько строк"
я могу в телеграме скинуть решение
Ок, @hiiamden .
Похожие вопросы
Предмет: Окружающий мир,
автор: восемь81
Предмет: Русский язык,
автор: ника8100
Предмет: Русский язык,
автор: itelman90
Предмет: Английский язык,
автор: pizzadict