Question

Пирамида пересечена плоскостью, параллельной основанию. Площадь основания равна 1521 дм2, а площадь сечения равна 9 дм2. В каком отношении, считая от вершины, плоскость сечения делит высоту пирамиды?

(Вводи сокращённое отношение!)

Высота пирамиды делится в отношении _ считая от вершины.

Answer 1

Ответ:

1:12

Объяснение:

Свойства сечения, параллельного основанию пирамиды:

если пирамиду пересекает плоскость, параллельная основанию, то

1. плоскость делит боковое ребро и высоту пирамиды на пропорциональные отрезки;

2. в сечении образуется многоугольник, подобный многоугольнику основания;

3. площади сечения и основания относятся как квадраты расстояний от них до вершины пирамиды.

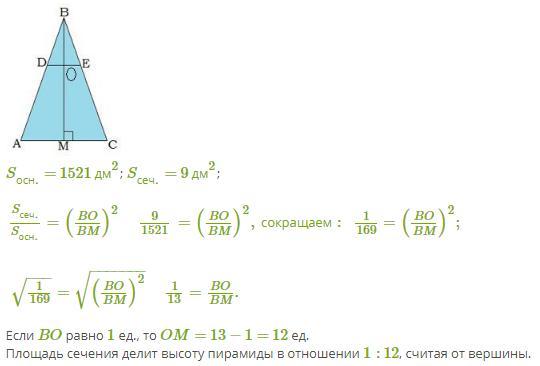
Решая задачу, независимо от того, какая пирамида дана и какое у неё основание, можно рисовать треугольник, в котором проведён параллельный основанию отрезок.

В этом случае важно видеть высоту пирамиды (на рис. MB — высота) и понимать, что за отрезком DE «скрывается» многоугольник сечения, а за AC — многоугольник основания.

 

Answer 2

Ответ:

1:12

Объяснение: