Question

основанием прямой призмы является прямоугольник со сторонами 8 и 12 см. диагональ меньшей боковой грани равна 10 см. Вычислите площади боковой и полной поверхности призмы

Answer 1

Ответ:

Sбок. =  240 (см²)

Sполн. = 320 (см²)

Объяснение:

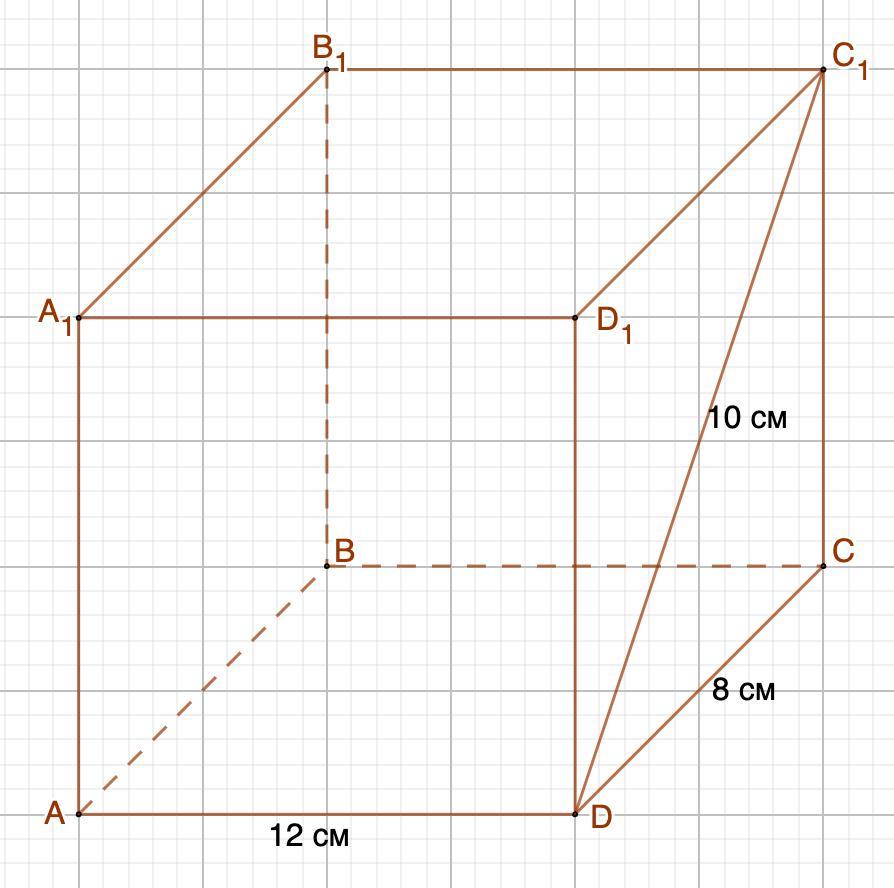
Дано: ABCDA₁B₁C₁D₁ - прямая призма.

АВ =CD = 8 см; AD = BC = 12 см; DC₁ = 10 см

Найти: Sбок., Sполн.

Решение:

У прямой призмы все боковые грани являются прямоугольниками.

Рассмотрим ΔDC₁C - прямоугольный.

По теореме Пифагора:

С₁С² = DC₁²-DC² = 10² - 8²= 36

⇒ C₁C = √36 = 6 (см)

Sбок. = Росн.· h, где h - высота призмы.

Sполн. = Sбок. + 2Sосн.

Площадь основания равна:

Sосн. = AD·DC = 12·8 = 96 (см²)

Периметр прямоугольника равен удвоенной сумме смежных сторон.

Росн. = 2(AD+DC) = 2(12+8) = 40 (см)

Sбок. = 40·6 = 240 (см²)

Sполн. = 240 + 40·2 = 320 (см²)