Предмет: Алгебра,
автор: XXXGNXXX
Даю максимум баллов! Нужна помощь! Просьба: напишите, пожалуйста, решение на листочке и сфоткайте его. Что бы оно выглядело так, как и должно быть. Спасибо. :)
Задание: упроситить
Приложения:
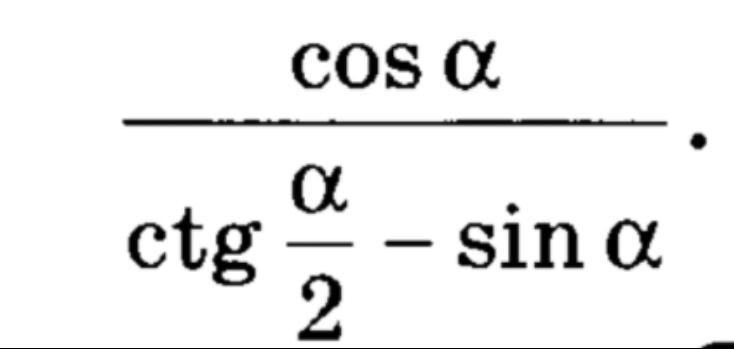
Ответы
Автор ответа:
1
Похожие вопросы
Предмет: Окружающий мир,
автор: Аноним
Предмет: Русский язык,
автор: limonolga04
Предмет: Русский язык,
автор: ZooMPlayRus
Предмет: Математика,
автор: Danjaa2014
Предмет: Биология,
автор: Vladgre4cko999