Предмет: Алгебра,
автор: tatyana0980
СРОЧНО, ДАЮ 100 БАЛЛОВ!
Вычислите интегралы (во вложениях)
Критерии:
1. Находит определенный интеграл многочлена
2. Находит определенный интеграл сложной тригонометрической функции
Приложения:
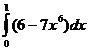
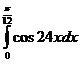
Ответы
Автор ответа:
0
Ответ:
Объяснение:
1) Интегрируем каждые слагаемые отдельно(свойство определённого интеграла):
Из таблицы:
Интеграл константы= константа*х, то есть будет 6х
Интеграл выражения в степени: число в степени на 1 больше делить на степень+1
У нас: 7 / 7 =
Собираем всё вместе:
6х - . Для того чтобы вычислить интеграл, нужно воспользоваться формулой Ньютона-Лейбница: F(b) - F(a), где F найденная функция, b- верхний предел (у нас 1), а-Нижний предел (у нас 0)
По формуле: 6*1- - 6*0- = 5.
Ответ: 5
2) Интегрируя сложную тригонометрическую функцию нужно взять обратное число числу около х, то есть 1/24 и проинтегрировать косинус. cosx = sinx - таблица
Получаем в пределах пи/12, 0.
Идём по той же формуле и получаем
zhekichoides:
прошу удалить этот ответ и не учитывать его
Хорошо, но жалобу на вас кидать не буду)
Я завтра с утра закреплю фото решение. И спасибо, большое, что без жалоб. Пытался с телефона формулы написать, жутко лагает и не редактируется текст.
Половина, к тому же, пропало...
Хорошо, если что, в профиле можете посмотреть ещё задачи, там все по 100 баллов
И если можете, то по раньше, завтра зачёт)
Похожие вопросы
Предмет: Английский язык,
автор: abylai77711
Предмет: Беларуская мова,
автор: Аноним
Предмет: Русский язык,
автор: Аноним
Предмет: Химия,
автор: karinazigula4
Предмет: Литература,
автор: daryaburbelo