Question

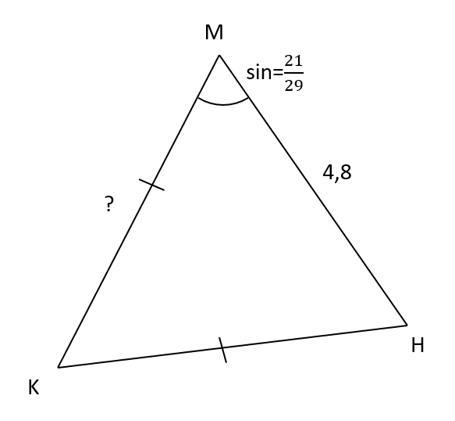
в треугольнике мнк известно, что мк=нк, мн=4,8 sinм=21/29 найти мк

Answer 1

Дано:

Δ MHK,

MK=HK

MH=4,8

sin ∠M =$\frac{21}{29}$

________

Найти:

МК —?

                                                Решение:

Δ MHK — равнобедренный, так как его боковые стороны равны.

Значит, ∠М = ∠Н, как углы при основании равнобедренного треугольника.

Сумма углов треугольника 180°.

Значит, ∠К = 180° - (∠М+∠Н) = 180° - 2∠М

Формула приведения:

sin (180° - α) = sin α

Получаем:

sin (180° - 2∠М) = sin 2∠М

Значит,

sin ∠К = sin 2∠М

Формула синуса двойного угла:

sin 2α = 2 ⋅ sin α ⋅ cos α

Получаем:

sin 2∠М = 2 ⋅ sin ∠М ⋅ cos ∠М

Основное тригонометрическое тождество:

$sin^2\alpha +cos^2\alpha =1$

Значит,

$sin\ 2 \angle M = 2\cdot sin\angle M \cdot \sqrt{1-sin^2\angle M}$

$sin\ 2\angle M = 2\cdot \frac{21}{29} \cdot \sqrt{1-({\frac{21}{29})}^2 } }$

$sin\ 2\angle M = 2\cdot \frac{21}{29} \cdot \frac{20}{29} =\frac{840}{841}$

$sin \angle K=\frac{840}{841}$

По теореме синусов, стороны треугольника пропорциональны синусам противолежащих углов.

$\frac{MH}{sin\angle K} =\frac{MK}{sin\angle M}$

$4,8:\frac{840}{841} =MK :\frac{21}{29}$

Разделить на дробь — значит умножить на обратную ей, поэтому:

$\frac{4,8 \cdot 841}{840}=\frac{MK\cdot 29}{21}$

Перекрестно умножаем:  

$4,8\cdot 841\cdot 21=MK\cdot 29\cdot 840$

Выразим МК:

$MK=\frac{4,8 \cdot \cancel 841 \cdot 21}{29 \cdot 840}$

Сократив 841 и 29 на 29, а 21 и 840 на 21, получаем:

$MK=\frac{4,8\cdot 29}{40}=\frac{139,2}{40}=3,48$

Ответ: МК = 3,48.