Предмет: Алгебра,
автор: NeoKokosik
3) решите уравнение.
помогите пожалуйста разобраться!! даю тридцать баллов.
Приложения:
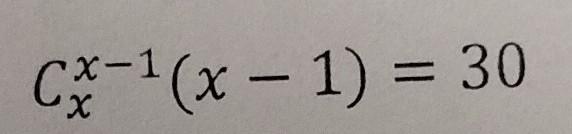
Ответы
Автор ответа:
1
Ответ:
Похожие вопросы
Предмет: Русский язык,
автор: dfrederiko
Предмет: Другие предметы,
автор: настюша233
Предмет: Английский язык,
автор: 123456789641
Предмет: Алгебра,
автор: pofigism
Предмет: Английский язык,
автор: Богдан29317