Предмет: Математика,
автор: RuslanRussia1881
Найти производные. Математика
Приложения:
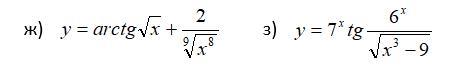
Ответы
Автор ответа:
1
Пошаговое объяснение:
ж)
з)
Приложения:

Аноним:
Записали производную arctg с таким аргументом, а внутренняя - степенная
Как-то не логичный переход получается , разве не согласны?
ну и в чем нелогичность?
https://prnt.sc/1y9xz58
Похожие вопросы
Предмет: Английский язык,
автор: ivanovaolgapo2
Предмет: Русский язык,
автор: Аноним
Предмет: Русский язык,
автор: тёмыч5550
Предмет: География,
автор: eserebrovap9y2ci
Предмет: Алгебра,
автор: aidanashanaxaeva