Предмет: Геометрия,
автор: Diana730
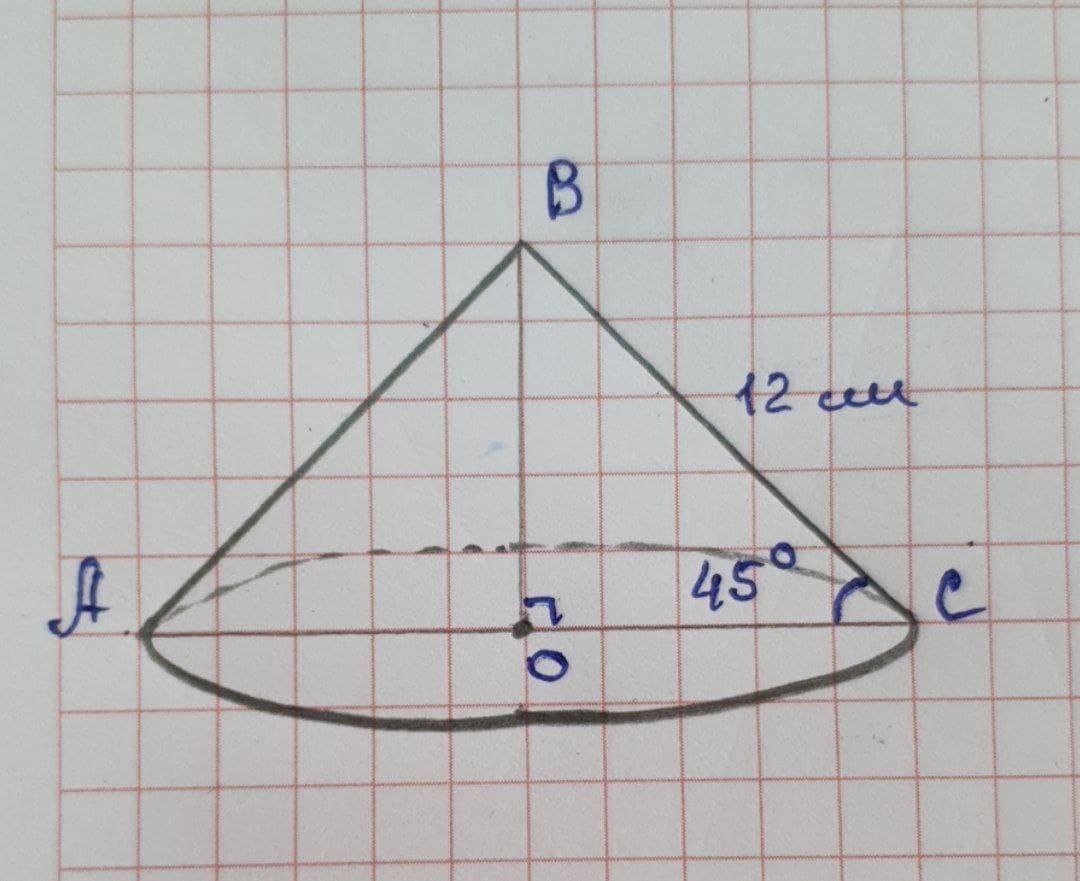
Образующая конуса 12 см, она составляет с плоскостью основания угол в 45°. Найти объем конуса и площадь боковой поверхности конуса
Ответы
Автор ответа:
1
Ответ:
V=144
S=72
Объяснение:
∠BOC=45°, BC=12см
Объем конуса равен одной трети произведения площади основания на высоту.
V=*
*r²*h
Формула площади боковой поверхности конуса:
S=*r*l
где r - радиус окружности основания,
l - длина образующей конуса.
ΔBOC(∠O=90°, т.к. ВО - высота конуса) : ∠С=∠В=45°. ΔBOC - равнобедренный. ⇒ ВО=ОС
BO=sin 45° * BC = √2/2 * 12 = 6√2
⇒h=r= 6√2
V=*
*r²*h =
*
* (6√2)²*6√2= 144
S=*r*l =
*6√2*12= 72
Приложения:
Похожие вопросы
Предмет: Другие предметы,
автор: irinalitina
Предмет: Русский язык,
автор: ульяша1705
Предмет: Русский язык,
автор: олбирльт
Предмет: Английский язык,
автор: 17711771li
Предмет: Математика,
автор: AndreyIvanov11