Предмет: Математика,
автор: RuslanRussia1881
Математика срочно помогите пожалуйста.
Приложения:
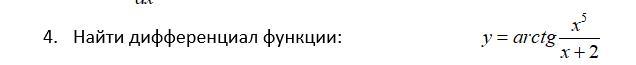
Ответы
Автор ответа:
1
Пошаговое объяснение:
Используем формулы:
Найдем f'(x):
Похожие вопросы
Предмет: Русский язык,
автор: 5843764
Предмет: Қазақ тiлi,
автор: Аноним
Предмет: Русский язык,
автор: оксана326
Предмет: Алгебра,
автор: safdagasw