Question

Решить Задание во вложении. С решением. 40 Балов

Answer 1

x²- (2a+1)+a²-4a+3=0

x²-(2a+1)+(a-3)(a-1)=0

во-первых, чтобы корни были, необходимо, чтобы дискриминант был ≥0

D= (2a+1)²-4(a²-4a+3)=4a²+4a+1-4a²+16a-12=

=20a-13≥0

при a≥13/20 уравнение будет иметь действительные корни

теперь вспомним теорему Виета

для приведенного уравнения

$( \: x_1 \: и \: x_2 - \\ корни \: нашего \: уравнения)$

$x_1•x_2=(a-3)(a-1) \\ </p><p>x_1+x_2=2a+1$

Для положительных корней

$x_1 \: и \: x_2 \:$

имеет место :

$x_1•x_2 > 0 \\ </p><p>x_1+x_2 > 0$

или

$(a - 3)(a - 1) > 0 \\ 2a + 1 > 0$

при условии а≥13/20

или

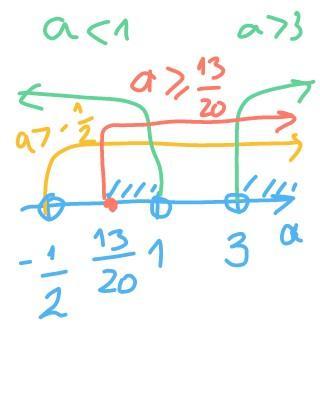
a>3 и а<1 ( зелёные области на графике)

а> -½ ( жёлтая область)

а≥13/20 ( красная область)

пересечением этих решений ( см рис)

будет

$a€ \: \: \: [\frac{13}{20} ,1)v(3 , + \infty )$

это и будут те значения а, при которых

корни уравнени будут положительны