Предмет: Алгебра,
автор: comarad
Достопочтимые Товарищи и Господа! Прошу вас о помощи, завтра срок сдачи
Упростите выражение:
Приложения:
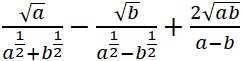
Ответы
Автор ответа:
1
Відповідь:
1
Пояснення:
Приложения:
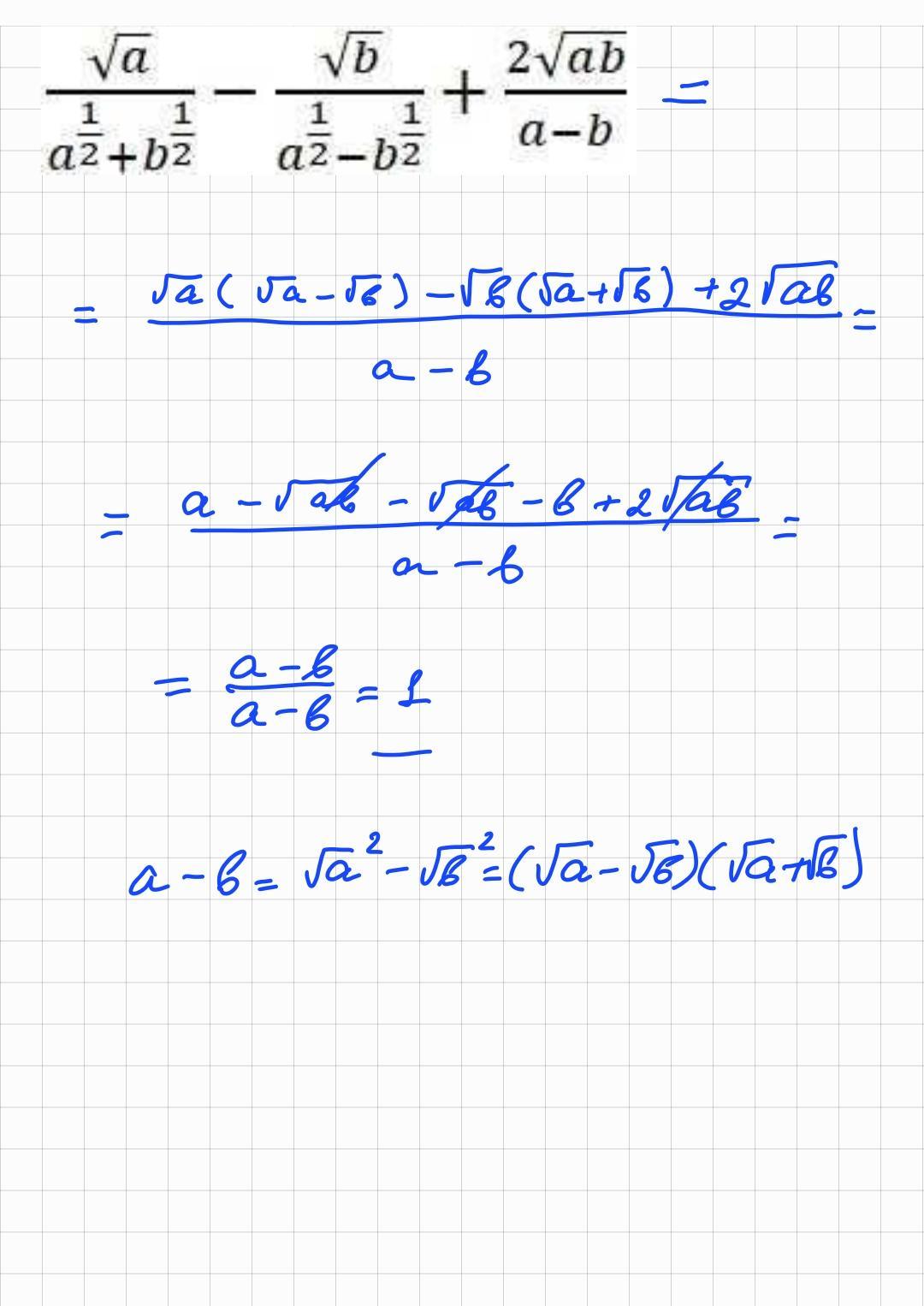
Автор ответа:
1
comarad:
Быть может это и немного нагло с моей стороны, однако не могли бы вы посмотреть мои Дз по геометрии?
Похожие вопросы
Предмет: Русский язык,
автор: harlamovamalvi1
Предмет: Русский язык,
автор: Аноним
Предмет: Українська мова,
автор: Igor3458395
Предмет: Математика,
автор: Eoriq30
Предмет: Математика,
автор: aleksaosipova