Предмет: Алгебра,
автор: Аноним
Помогите, пожалуйста, срочно!
Вычислить определенный интеграл с точностью α = 0,001, представив подынтегральную функцию в виде степенного ряда.
Приложения:
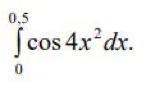
Ответы
Автор ответа:
0
Ответ:
Похожие вопросы
Предмет: Окружающий мир,
автор: iloveMaksik
Предмет: Английский язык,
автор: pipkina1973
Предмет: Русский язык,
автор: марианна41
Предмет: Информатика,
автор: pacixor
Предмет: Литература,
автор: 07772