Question

ПОМОГИТЕ ПОЖАЛУЙСТА ​

Answer 1

Ответ:

$|\overline{AB}|=2\ \ ,\ \ \ \angle{ABF}=30^\circ \ \ \ \ \ \Rightarrow \ \ \ |\overline{AF}|=\dfrac{1}{2}\cdot |\overline{AB}|=1\\\\\\|\overline{BF}|^2=|\overline{AB}|^2-|\overline{AF}|^2=2^2-1^2=4-1=3\ \ ,\ \ \ |\overline{BF}|=\sqrt3\ \ ,\\\\\angle{ABF}=30^\circ \ \ \ \Rightarrow \ \ \ \angle{(\overline{AB}\, ;\, \overline{BF})}=180^\circ -30^\circ =150^\circ \\\\\overline{AB}\cdot \overline{BF}=|\overline{AB}|\cdot |\overline{BF}|\cdot cos150^\circ =2\cdot \sqrt3\cdot (-\dfrac{\sqrt3}{2})=-3$

Answer 2

Скалярное произведение двух векторов $\vec{a}$ и $\vec{b}$ находится по формуле $\vec{a} × \vec{b} = | \vec{a} | × | \vec{b} | × cos \alpha$, где $\alpha$ — угол между векторами $\vec{a}$ и $\vec{b}$.

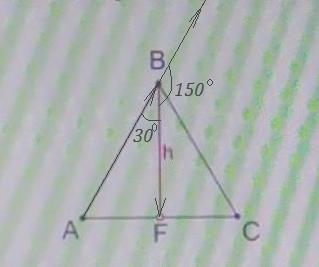
Чтобы найти угол между векторами, вектора нужно отложить от одной точки. В нашем случае, например, от точки B, для этого продолжаем прямую AB так, чтобы получилась прямая $ABB_1$ и откладываем от точки B вектор $\vec{AB}$ на продолжении прямой, тогда угол между векторами будет $∠FBB_1$, он смежный углу ABF => $∠FBB_1 = 180° – ∠ABF$ .

Вектором в модуле ( $| \vec{a} |$) обозначается длина вектора $\vec{a}$. Длина вектора $\vec{a}$ — это та же длина отрезка $a$.

Итак, составим нашу формулу:

$\vec{AB} × \vec{BF} = | \vec{AB} | × | \vec{BF} | × cos ∠FBB_1 = AB × BF × cos ∠FBB_1$

Решение.

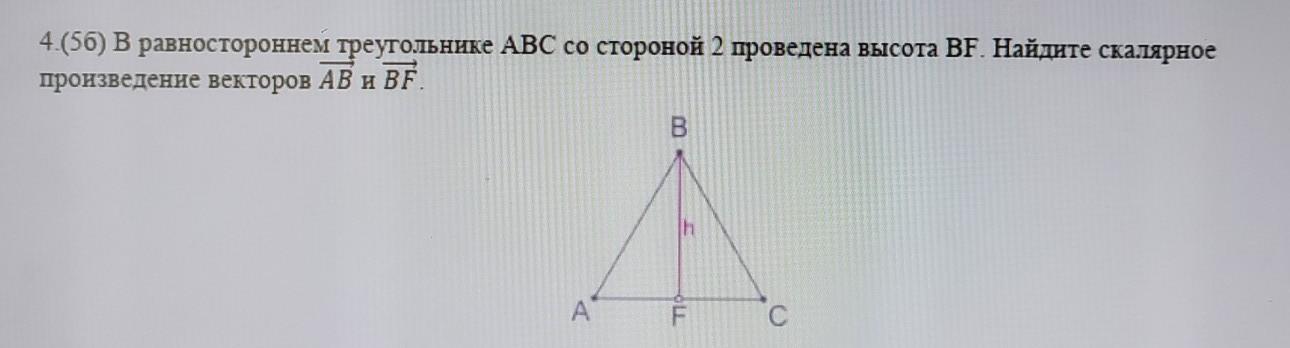
Треугольник ABC — равносторонний со сторонами равными 2 => AB = BC = AC = 2;

в равностороннем треугольнике все углы равны и равны 60° => ∠BAC = ∠ACB = ∠ABC = 60°.

BF — высота, проведённая к стороне AC => BF⊥AC => ∠AFB = ∠BFC = 90°.

Рассмотрим треугольник ABF.

Сумма углов треугольника равна 180° => ∠BAF (он же ∠BAC) + ∠AFB + ∠ABF = 180°,

∠ABF = 180° – ∠BAF – ∠AFB = 180° – ∠BAC – ∠AFB = 180° – 60° – 90° = 30°.

$∠FBB_1$ = 180° – ∠ABF = 180° – 30° = 150°.

Треугольник ABF — прямоугольный треугольник (∠AFB = 90°), поэтому к нему можно применить такое свойство: в прямоугольном треугольнике катет, лежащий против угла 30°, равен половине гипотенузы. Катет, лежащий против угла 30° — AF, гипотенуза лежит против угла 90° — AB.

=> AF = $\frac{1}{2}$ AB = $\frac{1}{2}$ × 2 = 1.

К прямоугольному треугольнику можно применить Теорему Пифагора: квадрат гипотенузы равен сумме квадратов катетов.

${AB}^{2} = {AF}^{2} + {BF}^{2}$,

${BF}^{2} = {AB}^{2} - {AF}^{2} = {2}^{2} - {1}^{2} = 4-1 = 3$,

$BF = \sqrt{3}$.

Итак, подставляем все значения в нашу формулу:

$\vec{AB} × \vec{BF} = AB × BF × cos ∠FBB_1 = 2 × \sqrt{3} × cos 150° = 2 \sqrt{3}× (- \frac{ \sqrt{3} }{2}) = - \frac{2 \sqrt{3} \sqrt{3} }{2} = - \frac{2 \times 3}{2} = - 3$

Ответ: - 3