Question

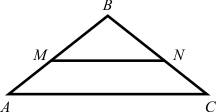
1. На рисунке2 MN || AC. а) Докажите, что AB•BN = СВ•ВМ. б) Найдите MN, если AM = 6 см, BM = 8 см, AС = 21 см. 
2. Даны стороны треугольников PQR и ABC: PQ = 16 см, QR = 20 см, PR = 28 см и АВ = 12 см, ВС = 15 см, АС = 21 см. Найдите отношение площадей этих треугольников.

Answer 1

1. Треугольники АВС и MBN подобны по двум углам
(угол В- общий; Угол ВМN  равен углу ВАС как соответственные при МN||АС и секущей АВ)
Треугольники подобны⇒сходственные стороны пропорциональны
АВ/ВМ=СВ/ВN ⇒AB•BN = СВ•ВМ
Б) АВ=АМ+МВ=6+8=14
МN/АС= ВМ/АВ; МN/21=8/14,  МN=21·8/14=12 (см)
Ответ МN=12см
2. Треугольники  PQR  и АВС подобны, т.к. стороны пропорциональны :
16/12=20/15=28/21=4/3
Площади подобных тругольников относятся как квадрат коэффициента подобия, т.е. как (4/3)²=16/9
площадь треугольника PQR относится к площади треугольника ABC
как 16 : 9

Answer 2

откуда во 2 номере 4/3

Answer 3

это отношение длин сторон 16/12=4/3

Answer 4

а ты сможеш ещё одну задачу решить пож

Answer 5

ПОМОГИТЕ ПОЖ На рисунке1 AB || CD. а) Докажите, что АО:ОС = BO:OD. б) Найдите АВ, если OD = 15 см, ОВ = 9 см, CD = 25 см.
2. Найдите отношение площадей треугольников ABC и KMN, если АВ = 8 см, BС = 12 см, АС = 16 см, КМ = 10 см, MN = 15 см, NK = 20 см.