Question

Модуль вектора a=8,
модуль вектора b=12,
угол фи=П/3.
Вектор c= 2a+1/2b.
Вектор d=1/2a-b.
Найти:
1.косинус альфа
2.Проекцию вектора d на вектор с
3.площадь параллелограмма.

Answer 1

Ответ:

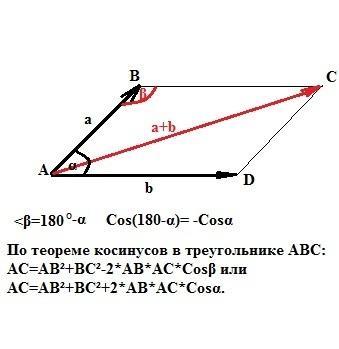
Найти модуль суммы векторов a и b.

если угол между векторами a и b равен α, то

по теореме косинусов

|a+b|=a²+b²+2abCosβ, где β=(180°-α) и Cosβ=-cosα.

В нашем случае |a+b|=9+64+2*3*8*(1/2)=97.

Пошаговое объяснение: