Помогите решить уравнение.
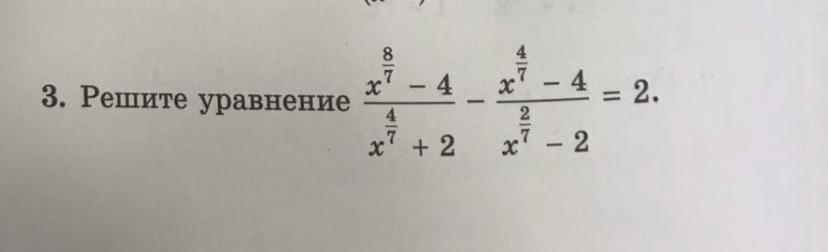
Ответы
a² - b² = (a - b)(a + b)
(a^2/7)^2 = a^4/7
(a^4/7)^2 = a^8/7
(x^8/7 - 4)/(x^4/7 + 2) - (x^4/7 - 4)/(x^2/7 - 2) = 2
x^2/7 ≠ 2
x ≠ 2^7/2
x > 0
(x^4/7 - 2)(x^4/7 + 2)/(x^4/7 + 2) - (x^2/7 - 2)(x^2/7 + 2)/(x^2/7 - 2) = 2
x^4/7 - 2 - (x^2/7 + 2) = 2
x^4/7 - x^2/7 - 6 = 0
x^2/7 = y
y^2 - y - 6 = 0
D = 1 + 24 = 25
y12 = (1 +- 5)/2 = 3 -2
y = -2 нет
y = 3
x^2/7 = 3
x = 3^7/2 = √3^7 = 27√3
Вводим замену: x^(2/7) = t. Это положительная величина.
((t^4 - 4) / (t^2 + 2)) - ((t^2 - 4) / (t - 2)) = 2. Раскроем разность квадратов.
((t^2 - 2) (t^2 + 2) / (t^2 + 2)) - ((t - 2)(t + 2)/(t - 2)) = 2.
Можно сократить дроби на (t^2 + 2) и (t - 2), при условии t > 2.
Получаем квадратное уравнение
t^2 - 2 - (t + 2) = 2 или t^2 - t - 6 = 0.
D = 1 - 4*1*(-6) = 25. √D = +-5.
t1 = (1 - 5)/2 = -2 не принимаем.
t2 = (1 + 5)/2 = 3.
Обратная замена: x^(2/7) = 3, отсюда x = 3^(7/2) ≈ 46,7654.
Ответ: х = 3^(7/2).