Question

Срочно!!!!
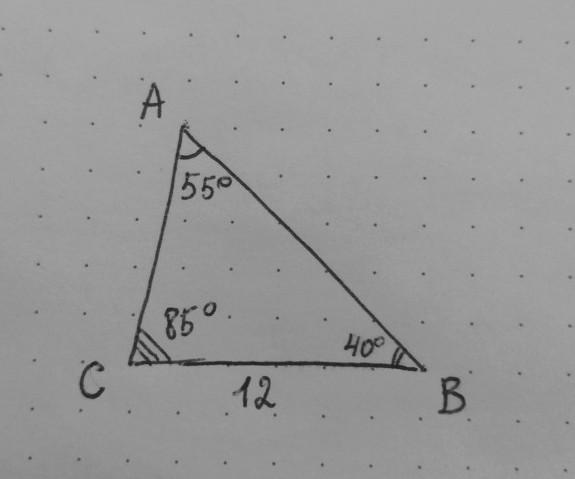
В треугольнике ABC сторона CB = 12; ∠A = 55°, ∠B = 40°. Определите длины сторон:

а) AB (15 баллов);

б) AC (15 баллов).

Для решения вам понадобится калькулятор, который вычисляет значения тригонометрических функций (или таблицы Брадиса). Приведите рисунок.

Answer 1

Сумма углов треугольника равна 180°,

∠A = 55°, ∠B = 40°, ∠C = 180° – (55° + 40°) = 85°.

По таблице Брадиса,

$sin \: 40° ≈ 0.6428,$

$sin \: 55° ≈ 0.8192,$

$sin \: 85° ≈ 0.9962$

Воспользуемся Теоремой синусов,

$\frac{sinA}{a} = \frac{sinB}{b} = \frac{sinC}{c}$

Выразим одну из сторон,

$a = \frac{b \times sinA}{sinB}$

Подставим наши значения,

$AC = \frac{CB \times sin \: 40°}{sin \: 55°} = \frac{12 \times 0.6428}{0.8192} ≈ 9.416$

$AB = \frac{AC \times sin \: 85°}{sin \: 40°} = \frac{9.416 \times 0.9962}{0.6428} ≈ 14.5927$

Ответ: AC ≈ 9.416; AB ≈ 14.5927