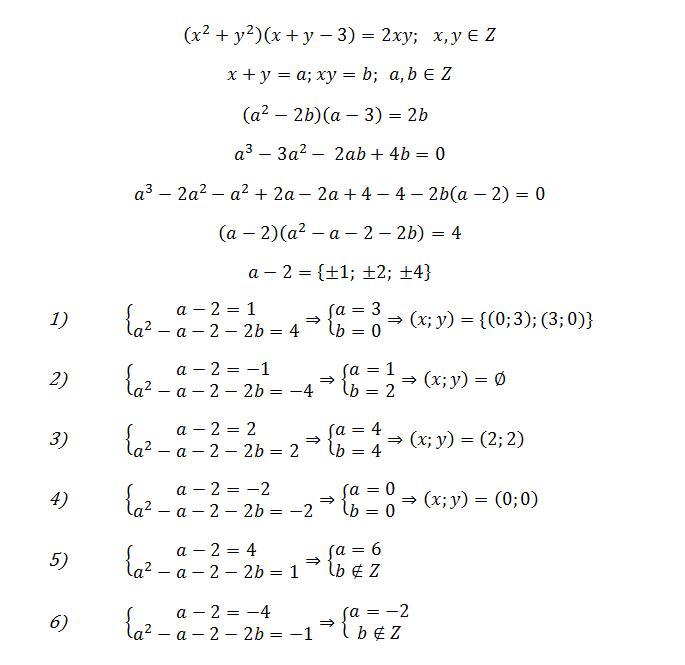Предмет: Алгебра, автор: Simba2017

решить в целых числах (продолжение):
(x^2+y^2)(x+y-3)=2xy
(вопрос создан для конкретного пользователя)

Simba2017: ок!
Simba2017: решение уже есть, предлагается другой способ решения
Simba2017: https://znanija.com/task/45160966
Simba2017: если у вас другой способ решения-пишите...
Simba2017: идея не моя...
kanmmu: Симба, я изложил свою идею в комменте к ответу mmb1. Если остались вопросы, с радостью отвечу.

Ответы

Автор ответа: mmb1
2

(x^2+y^2)(x+y-3)=2xy

1. виден сразу первый ответ x = 0 y = 0

x² + y²= 0  xy = 0

2. рассмотрим x = 0

y²(y - 3) = 0

y = 0

y = 3

3. рассмотрим y = 0

x²(x - 3) = 0

x = 0

x = 3

4. рассмотрим x ≠ 0 y ≠ 0

x, y > 0 одного знака

так как x+y-3  целое и xy ≠ 0 , то поделив на xy лево и право получим

(x^2+y^2)(x+y-3)/xy=2xy/xy

(x/y + y/x)(x + y - 3) = 2

x/y + y/x - целое и ≥ 2

x + y - 3 целое и  > 0 и < 2

значит

x/y + y/x = 2

x + y - 3 = 1

----

(x - y)² = 0

x + y = 4

----

x = y

x = 2  y = 2

5. рассмотрим x ≠ 0 y ≠ 0

x, y < 0 одного знака

так как x^2+y^2 > 0  2xy > 0

а (x + y - 3) < 0

решений нет

6. рассмотрим x ≠ 0 y ≠ 0

x, y разных знаков

так как x+y-3  целое и xy ≠ 0 , то поделив на xy лево и право получим

(x^2+y^2)(x+y-3)/xy=2xy/xy

(x/y + y/x)(x + y - 3) = 2

(x/y + y/x) - целое и ≥ -2

x + y - 3 целое и  < 0 и > -2

значит

-(x/y + y/x) = 2

x + y - 3 = -1

----

(x + y)² = 0

x + y = 2

----

x = -y

0 = -2 решений нет

ответ (0,0) (0,3) (3,0) (2,2)

kanmmu: Поскольку не успел добавить свое решение, покажу идею на базе Вашего, так как первые три пункта у нас идентичны. Начиная с 4, я рассуждал иначе. У нас имеется произведение двух целых чисел, оно равно 2. Целые делители 2: +-1 и +-2, причем первая скобка по модулю >=2 (как взаимнообратные), а значит она равна по модулю 2 при х=у. Значит нужно рассмотреть 2 тривиальных случая: 2×1 и (-2)×(-1).
igorShap: А почему слева произведение целых чисел? Ведь из того, что (x + y - 3) целое не следует напрямую, что и (x/y + y/x) тоже целое. [1/4*8=2 - 1/4 не целое]
kanmmu: Я же указал, что в первой скобке сумма взаимнообратных чисел, которая по модулю не меньше 2. Случай когла больше нам не подойдет, иначе вторая скобка по модулю будет меньше 1, что невозможно, так как х,у-целые.
igorShap: А, это понятно. Но у Вас в комментарии это идет в обратном порядке: сначала Вы говорите, что оба числа целые, а уже потом рассматриваете делители и оценку ) Отсюда и возник вопрос
kanmmu: Прошу прощения. Просто изначально коммент получился длинный и не добавлялся. Пришлось урезать, не обратил внимания, что логика нарушилась)
Автор ответа: guvanch021272
2

Ответ:

(0;0); (0;3); (3;0); (2;2)

Объяснение:

Приложения:
kanmmu: Я тоже изначально сделал такую замену, но можно проще. В предыдущем ответе моя идея, но сырая.
kanmmu: У меня после рассмотрения тривиальных х=0 и у=0 нужно перебрать только 2 случая, поэтому и ушёл от замены.
Simba2017: опять вам не хватило ответа...
kanmmu: Да уж! За товарищами не поспеть)
Предыдущий вопрос
Следующий вопрос
Похожие вопросы
Предмет: Окружающий мир, автор: лизки1
Какой цветок был подарен человеку богами, чтобы покорить сердце девушки
1 год назад
Предмет: Английский язык, автор: daryashishkina
плиз помогите решить задание по английскому очень надо!!!
Choose the right preposition
1. It’s very nice … you to let me use your car.
a). on b). of c). in d). off
2. I’m not very good … repairing things.
a). at b). on c). in d). with
3. Linda is married… an American.
a).on b).in c). at d). to
4. Are you afraid …dogs?
a). of b). at c). on d). about
5. Jill starts her new job on Monday. She’s quite excited … it.
a). with b). about c). at d). on
6. I’m sorry …. the noise last night. We were having a party.
a). with b). on c). about d). of
7. Kazan is famous ….its Universiade – 2013.
a). for b). with c). of d) in
8. Who was responsible ….all that noise?
a). of b). with c). in d). for
9. Are you interested… art?
a). in b). at c). on d). of
10. We had many tests, so I was very tired …. doing homework.
a). off b). of c). with d). about
11. Mary is very fond…music. She goes to music school four times in a week.
a). in b). on c). of d). at
12. The letter I wrote was full….. mistakes.
a). off b). with c). on d). of
13. Who does this coat belong…?
a). to b). with c). in d).at
14. Do you believe… God?
a). on b). about c). in d).at
15. I complained … missing a taxi.
a). of b). about c).at d). with
16. The advantage …living alone is that you can do what you like.
a). about b). of c). in d). on
17. He always keeps a photograph …his wife in his wallet.
a). with b).in c). of d). off
18. Did you get an invitation… the party?
a). to b). in c). on d). with
19. His attitude … his job is very negative.
a). on b). in c). with d). towards
20. Do you have a good relationship … your parents?
a). to b). between c). with d). on
21. There are some differences… British English and American English.
a). between b). among c). on d).with
22. His reaction …my suggestion was not very enthusiastic.
a). to b). on c). in d). over
23. Tom’s away at the moment. He is … holiday in France.
a). in b). on c). over d). at
24. After work we went to a café …a drink.
a). on b). to c). for d). with
25. What did you have ….lunch?
a). for b). in c). at d). on
1 год назад
Предмет: Русский язык, автор: wwe555
укажите стиль речи и ведущий тип речи текста )))))))))))))))На одной из старинных улиц Москвы стоит особняк, построенный после пожара 1812 года. Здесь
находится музей Пушкина, давно знакомый москвичам и гостям столицы.
В начале прошлого века это был гостеприимный литературный дом. Сюда приходили многие известные люди: Жуковский, Карамзин, Батюшков. Сегодня они смотрят на нас с портретов, а когда-то смотрели на маленького Пушкина. Произведения прославленных русских художников: Рокотова, Кипренского, Тропинина и других — украшают многие залы музея. Здесь вы увидите и миниатюрную работу неизвестного художника, изображавшую Пушкина-мальчика, и другие портреты, созданные при жизни поэта.
Первый зал музея посвящен тем историческим истокам, которые питали его творческий гений. В следующем зале пушкинская эпоха представлена в историческом и обыденном, великом и малом, трагическом и забавном: батальные сцены и модные картинки, правительственные документы и письма частных лиц. Портреты русских царей, великих полководцев, известных писателей соседствуют с портретами тех, чьи имена остались неизвестными. Так в музее начинается путешествие в пушкинское время, рассказ о Пушкине.ста ))
1 год назад
Предмет: Геометрия, автор: Aksana2017
Помогите пожалуйста.
треугольник АВС, АВС = 42°. Найдите градусную меру угла BAС.


Вопрос 5:

В треугольнике АВС (С = 90 °) А = 30°, ВС = 12 см

Найдите длину гипотенузы АВ.

Вопрос 6: В равнобедренном треугольнике АВС с основанием ВС проведена высота АD. Найдите величины углов В и С, если боковая сторона треугольника АС=7 см, а СD=3,5 см

Вопрос 7: В прямоугольном равнобедренном треугольнике гипотенуза равна 18 см. Определите высоту треугольника, опущенную из вершины прямого угла
7 лет назад
Предмет: Математика, автор: Светлана200691
помогите пожалуйста ответить на 8 9 и 10 вопросы. Дам 20 баллов
7 лет назад