Предмет: Геометрия,
автор: svetadermidonova
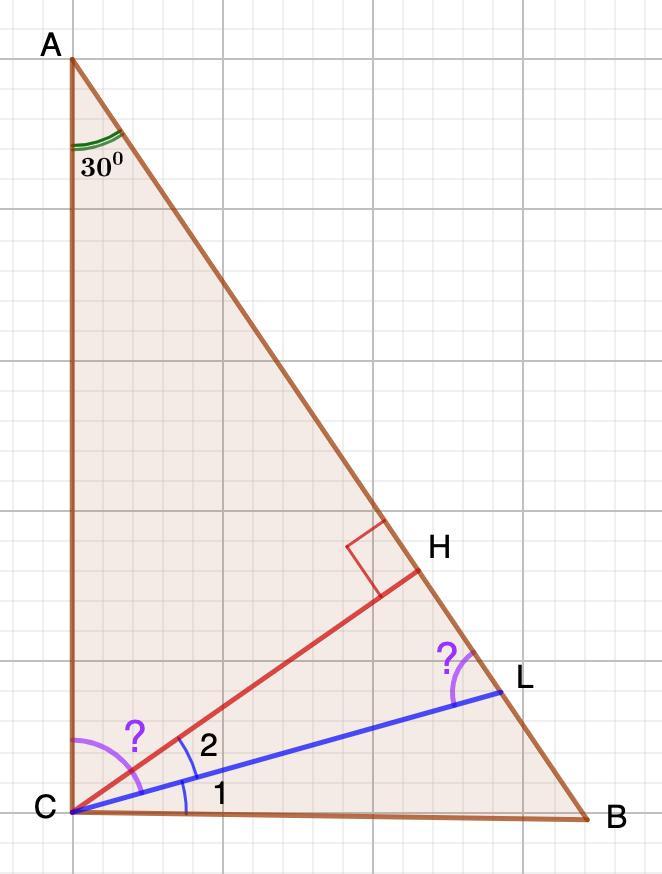
В прямоугольном треугольнике ABC угол A равен 30 градусов. Из вершины прямого угла C проведена высота CH. CL-биссектриса треугольника HBC. Найти градусные меры угла ACL И ALC
Помогите емае
Приложения:

Ответы
Автор ответа:
3
Ответ:
∠ACL=75°; ∠ALC=75°
Объяснение:
Дано: ΔАВС - прямоугольный;
∠А=30°
СН - высота; СL - биссектриса ΔНВС.
Найти: ∠АСL; ∠ALC.
Решение:
1. Рассмотрим ΔАНС - прямоугольный.
∠АСН=90°-∠А (сумма острых углов прямоугольного Δ-ка)
∠АСН=90°-30°=60°
2. Рассмотрим ΔСНВ - прямоугольный.
∠СНВ=∠С-∠АСН=90°-60°=30°
⇒∠1=∠2=30°:2=15° (CL - биссектриса)
3. ∠ACL=∠ACH+∠2=60°+15°=75°
4. Рассмотрим ΔСНL - прямоугольный.
∠СLН=90°-∠2=90°-15°=75° (сумма острых углов прямоугольного Δ-ка)
⇒ ∠ALC=75°
Приложения:
Похожие вопросы
Предмет: Окружающий мир,
автор: vnfdbngcc
Предмет: Русский язык,
автор: придумай2
Предмет: Английский язык,
автор: влада20062
Предмет: Математика,
автор: натан2002
Предмет: Другие предметы,
автор: ангелина1056