Предмет: Математика,
автор: iribelik2015
найти указанные пределы
Приложения:
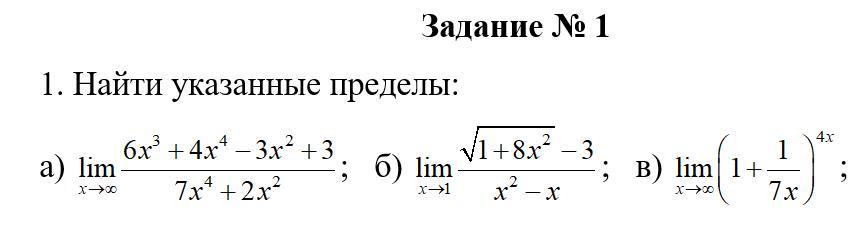
Ответы
Автор ответа:
1
Ответ:
Пошаговое объяснение:
a) поделим числитель и знаменатель на переменную в наивысшей степени знаменателя
б) чтобы избавиться от 0 в знаменателе домножим знаменатель и числитель на выражение сопряженное к числителю
в) здесь используем свойства второго замечательного предела
у нас а = 1
b = 4/7
тогда
Похожие вопросы
Предмет: Окружающий мир,
автор: phimka
Предмет: Русский язык,
автор: 160678
Предмет: Русский язык,
автор: Александра1706
Предмет: Право,
автор: 839010
Предмет: Қазақ тiлi,
автор: darikow79