Предмет: Математика,
автор: Viva8888
Найти значение производной функции
Приложения:
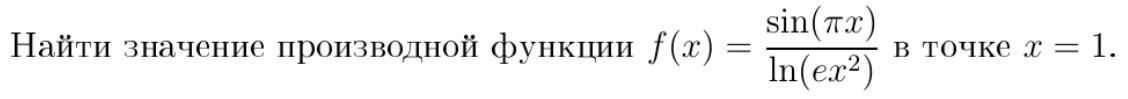
Ответы
Автор ответа:
1
Ответ:
Пошаговое объяснение:
resheno
Приложения:

Автор ответа:
2
Ответ:
NNNLLL54:
см
Похожие вопросы
Предмет: Русский язык,
автор: kkkkk8888
Предмет: Технология,
автор: ВикторияVD
Предмет: Русский язык,
автор: yliyaborisova1986
Предмет: Геометрия,
автор: НЕВЕСОМАЯ67
Предмет: Химия,
автор: greenbv