Предмет: Алгебра,
автор: kirilukm992
Помогите решить 5 и 6 задание
Приложения:
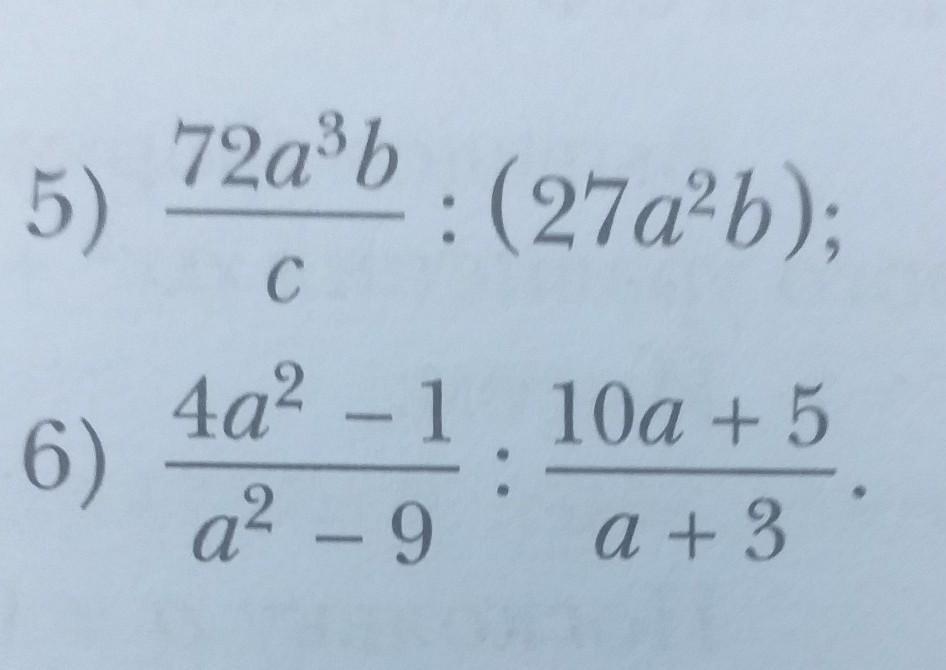
Ответы
Автор ответа:
0
Объяснение:
5)
6)
Автор ответа:
2
Ответ:
Объяснение:
Похожие вопросы
Предмет: Окружающий мир,
автор: алымбек2
Предмет: Русский язык,
автор: eldanainurdina
Предмет: Английский язык,
автор: kontzova2015
Предмет: Русский язык,
автор: hangfum