Предмет: Алгебра,
автор: shushablinchik
Помогите пожалуйста, дам 30 баллов и лучший ответ
Приложения:
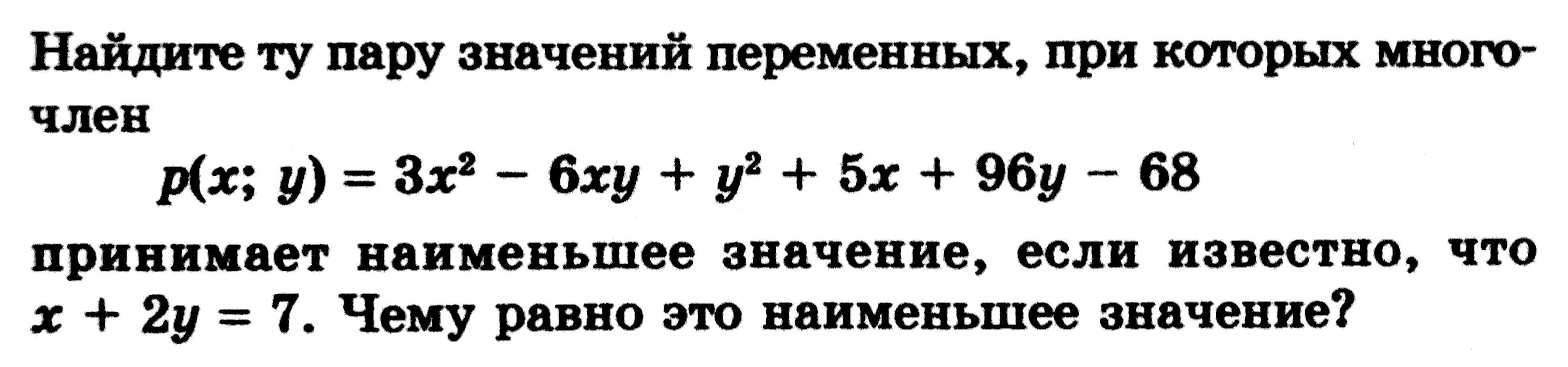
Simba2017:
подставьте у через х-получите функцию одной переменной
там вероятно парабола-вершина ее находится через коэффициенты функции
Ответы
Автор ответа:
0
Ответ:
x = 5,4; y = 0,8; p(x,y) = 98
Объяснение:
p(x, y) = 3x^2 - 6xy + y^2 + 5x + 96y - 68
Известно, что x + 2y = 7, отсюда
x = 7 - 2y
Подставим это в функцию
p(y) = 3(7 - 2y)^2 - 6y(7 - 2y) + y^2 + 5(7 - 2y) + 96y - 68
p(y) = 3(4y^2 - 28y + 49) - 42y + 12y^2 + y^2 + 35 - 10y + 96y - 68
p(y) = 25y^2 - 40y + 114
Нам нужно найти наименьшее значение, возьмём производную и приравняем ее к 0.
p'(y) = 50y - 40 = 0
y = 40/50 = 4/5 = 0,8
p(0,8) = 25(0,8)^2 - 40*0,8 + 114 = 25*0,64 - 32 + 114 = 16 - 32 + 114 = 98
x = 7 - 2y = 7 - 2*0,8 = 7 - 1,6 = 5,4
5-9 класс производную не знают
Тогда надо выделять полные квадраты, а это не так просто.
да нет, x0=-b/(2a)=40/50=0.8-вершина параболы
Как это? Функция же зависит от х и от у.
Здесь одним х0 не обойдешься.
А, вы про функцию уже после подстановки! Тогда да, согласен. Дали бы исправить...
Похожие вопросы
Предмет: Окружающий мир,
автор: Неизвестный341
Предмет: Русский язык,
автор: Yoga13
Предмет: Русский язык,
автор: LENKA105
Предмет: Русский язык,
автор: GDragon123
Предмет: Английский язык,
автор: retuprp