Предмет: Геометрия,
автор: Аноним
Помогите пожалуйста решить!!!
Найдите площадь закрешонного треугольника?
Приложения:
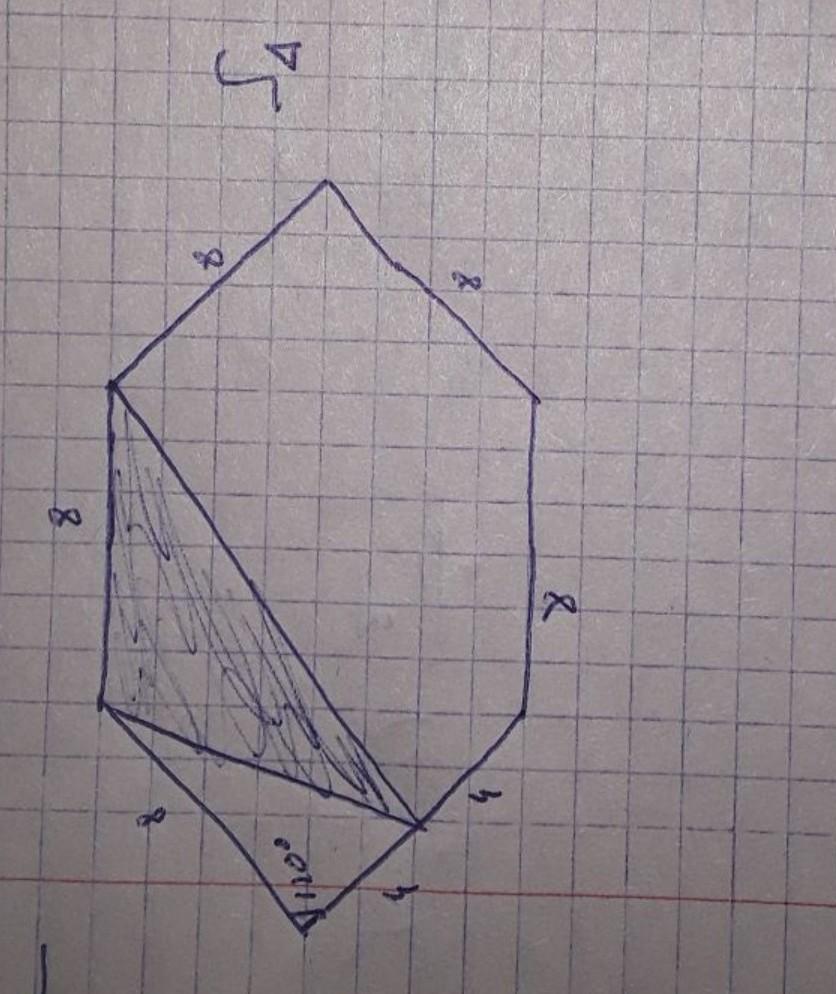
kanmmu:
24×3^(1/2)
Задачка устная. Чертить не могу, а по Вашему рисунку написать понятное решение проблемно. Главное увидеть правильный шестиугольник, и тогда проблем с решением не возникнет.
да уж. Даже буквы не догадались поставить
Ответы
Автор ответа:
4
Ответ:
24√3 ед²
Объяснение:
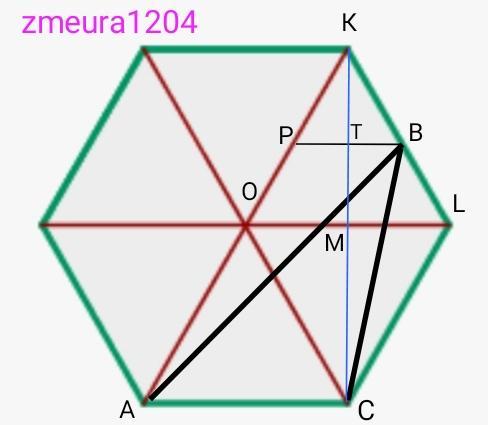
Правильный шестиугольник.
Диагонали правильного шестиугольника образуют 6 равносторонних треугольников.
Рассмотрим треугольник ∆ОКL
KM- высота, биссектрисса и медиана треугольника ∆ОКL.
По формуле нахождения высоты равностороннего треугольника
KM=KL√3/2 ед
KM=8√3/2=4√3 ед
Так как ВL=KB, по условию
Применяем теорему Фалеса
КТ=ТМ
ТМ=КМ/2=4√3:2=2√3 ед
Рассмотрим треугольник ∆ОLC
CM- высота, биссектрисса и медиана треугольника ∆ОLC.
Поскольку ∆ОLC=∆OKL, то и высоты их равны КМ=МС=4√3 ед
ТС=ТМ+КМ=2√3+4√3=6√3 ед
ТС- высота ∆АВС опущенная на сторону АС.
S(∆ABC)=1/2*AC*TC=1/2*8*6√3=24√3 ед²
P.S. поскольку еденицы измерения не указаны, то написала ед.- едениц.
Приложения:
Ну, поставьте нарушение.
Как зачем? Ответ же, не правильный.
значит ВЫ рассуждали просто так?
Формально, конечно, guvanch021272 прав. Условие неполное. Но на мой взгляд применительно конкретно к этой задаче "домыслить" условие можно причём вопрошающему решение помогло.
Похожие вопросы
Предмет: Окружающий мир,
автор: annamarkarova
Предмет: Русский язык,
автор: ученик200407
Предмет: Окружающий мир,
автор: gukasyan06
Предмет: Биология,
автор: private09
Предмет: Литература,
автор: Elinka990