Предмет: Алгебра,
автор: Аноним
Помогите пожалуйста решить!!!
Сколько имеет корни?
Приложения:
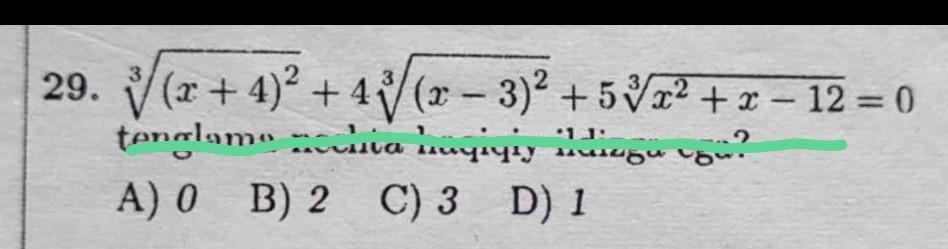
otveti8class:
не получается ответьть,но ответ вроде 3
Ответы
Автор ответа:
1
Ответ:
B) 2
Объяснение:
Пусть
Тогда уравнение имеет вид
ИЛИ
Уравнение имеет два корня.
Похожие вопросы
Предмет: Русский язык,
автор: ученик200407
Предмет: Окружающий мир,
автор: gukasyan06
Предмет: Английский язык,
автор: CoolMann
Предмет: Литература,
автор: Elinka990
Предмет: География,
автор: Аноним