Предмет: Алгебра,
автор: benlinus130
Koличecтвo кopнeй уpaвнeния  , пpинaдлeжaщих oтpeзкy [-3;3], paвнo
, пpинaдлeжaщих oтpeзкy [-3;3], paвнo
Ответы
Автор ответа:
1
Ответ:
равно 3
Объяснение:
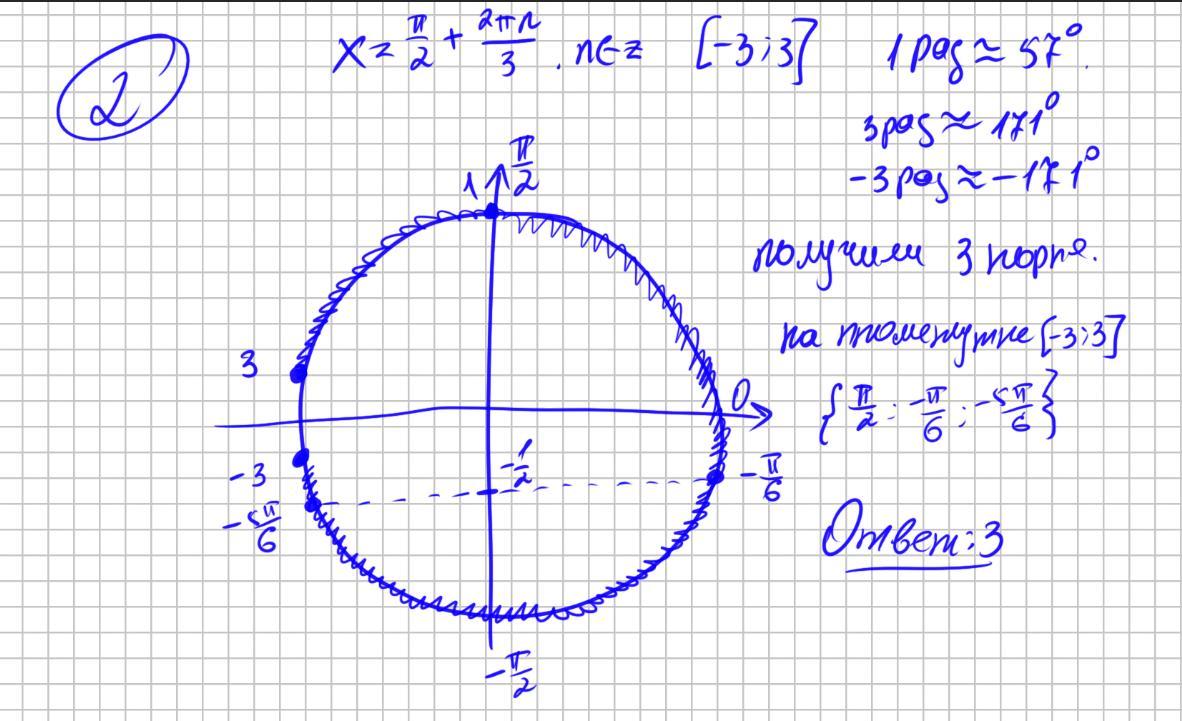
На фото два способа отбора корней.
1) Через двойное неравенство
2) Через тригонометрический круг.
Приложения:

Автор ответа:
1
Ответ : 3 корня
Похожие вопросы
Предмет: Русский язык,
автор: Мяня1
Предмет: Другие предметы,
автор: ЛИЗАТАММ
Предмет: Русский язык,
автор: умница906
Предмет: Русский язык,
автор: самур2
Предмет: ОБЖ,
автор: dctcfyfcyCv