Предмет: Алгебра,
автор: okc0677
Решите срочно математику, пожалуйста!!!
Приложения:
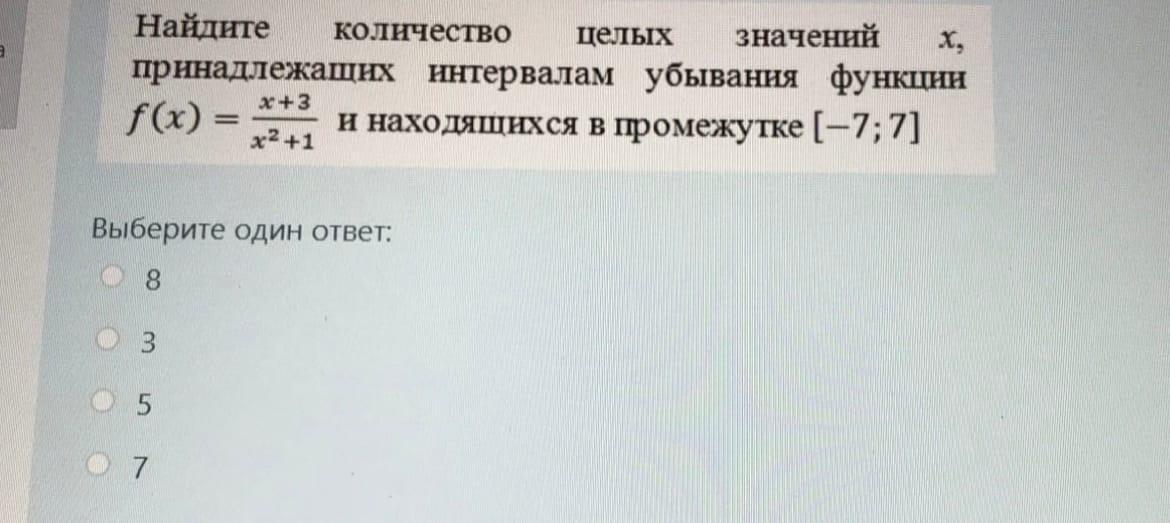
Ответы
Автор ответа:
2
- + -
[-7]_____ - 3 - √10_______ √10 - 3____[7]
↓ ↑ ↓
x ∈ [- 7 ; - 3 - √10] ∪ [√10 - 3 ; 7]
Ответ : 8
Похожие вопросы
Предмет: Русский язык,
автор: лучик8
Предмет: Окружающий мир,
автор: danka18
Предмет: Русский язык,
автор: xthtgeuf
Предмет: Математика,
автор: timoxa2006t
Предмет: Қазақ тiлi,
автор: murka280705