Question

дана квадратичная функция
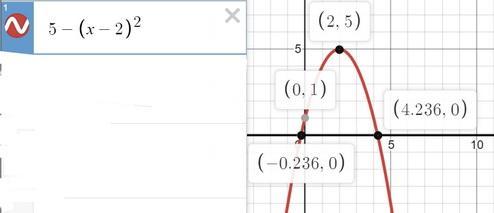
f( x )=5-(x-2)^2

Найдите точки пересечения с осями и вершиной соответствующей параболы и нарисуйте график функции

Answer 1

Ответ:

Пошаговое объяснение:

$\displaystyle y(x) = 5-(x-2)^2$

приведем уравнение к общему виду

$\displaystyle y(x) = -x^2+4x-4+5 = -x^2+4x+1$

это парабола ветвями вниз

найдем вершину параболы

$\displaystyle x_0=\frac{-b}{2a} =\frac{-4}{-2} =2\\y_0(2)=5-(2-2)^2=5$

координаты вершины параболы (2; 5)

пересечение о оу (х=0)

у(0) = 5-(0-2)² = 1

точка пересечения с осью оу (0; 1)

пересечение с осью ох (у=0)

0= -x² +4x +1

$\displaystyle \\D=\sqrt{20} =2\sqrt{5} \\\\\displaystyle x_{1,2}=\frac{-4\pm2\sqrt{5} }{-2} =2\pm\sqrt{5} \\\\x_1= 2-\sqrt{5} \approx -0.2\\\\x_2=2+\sqrt{5} \approx 4.2$

точки пересечения с осью ох ( 2 -√5; 0)  и  (2 +√5; 0)