Предмет: Алгебра,
автор: hghyf25vhh
Задание на картинке ⬆️⬆️⬆️
Приложения:
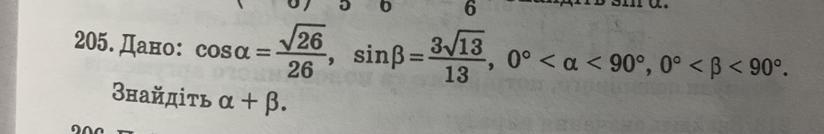
Ответы
Автор ответа:
1
Объяснение:
см фото,,,,,,,,,,,,,,,,,,,,,
Приложения:

hghyf25vhh:
Вы можете помочь ещё с одним заданием у меня в профиле
Пожалуйста
Автор ответа:
1
Ответ:
45°
Объяснение:
два последних члена известны, найдём первые два
Подставляем всё в формулу
Вы можете помочь ещё с одним заданием у меня в профиле
Пожалуйста
Похожие вопросы
Предмет: Русский язык,
автор: УльянаЗима
Предмет: Русский язык,
автор: Misha0566
Предмет: Русский язык,
автор: maqdi1
Предмет: Музыка,
автор: ånumėшнuk
Предмет: Алгебра,
автор: шрщорзо