Предмет: Алгебра,
автор: svetnik06121964
Изобразить на координатно прямой множество точек, удовлетворяющих условию:
{ | x-2| = 3
{ |y|<4
pushpull:
я решила эту задачу здесь https://znanija.com/task/45126011
Ответы
Автор ответа:
0
Ответ:
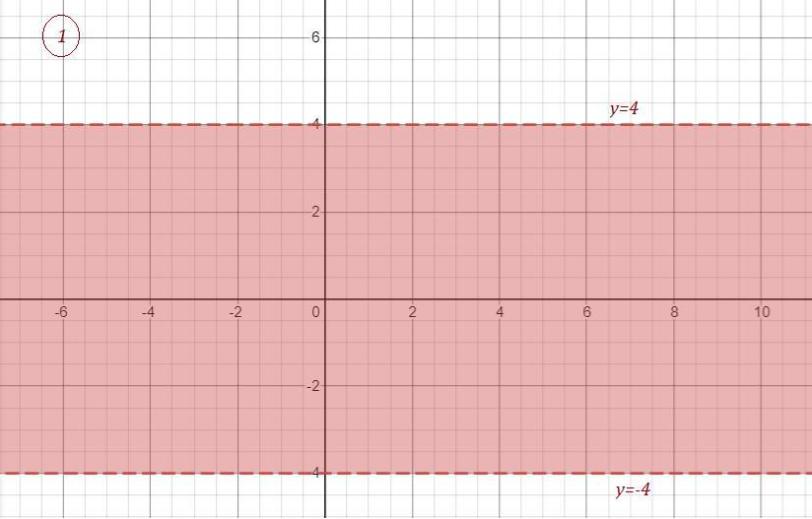
Неравенство -4<y<4 задаёт полосу между прямыми у=4 и у= -4 , причём сами прямые не входят в эту полосу, так как неравенство строгое . Рисунок 1 .
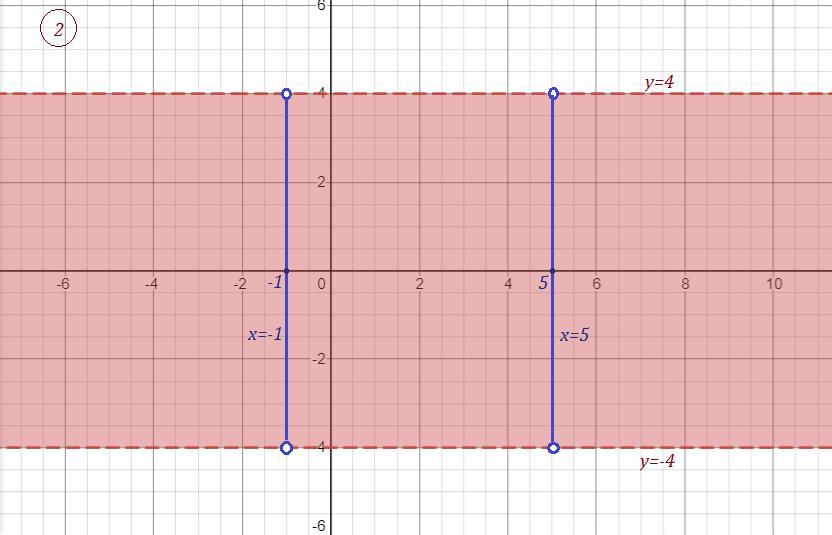
От прямыx х=5 и х= -1 надо оставить те их части, которые находится в полосе -4<y<4 , причём точки (-1;4) , (5;4) , (-1;-4) , (-1;5) не принадлежат получившимся отрезкам . Рисунок 2 .
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: Milenchik13
Предмет: Русский язык,
автор: SkyMaks2
Предмет: Английский язык,
автор: Kiskag
Предмет: Другие предметы,
автор: batia4923p6g7mn