Предмет: Математика,
автор: Hard8968
найти все значения параметра а, при котором уравнение х+√(16-х^2) = a имеет единственное решение, напишите решение, пожалуйста
mathgenius:
Удобная замена: x = 4cos(t)
верно с учетом ОДЗ
Хотя лучше решать все же графически: t = sqrt(16 - x^2) >= 0.
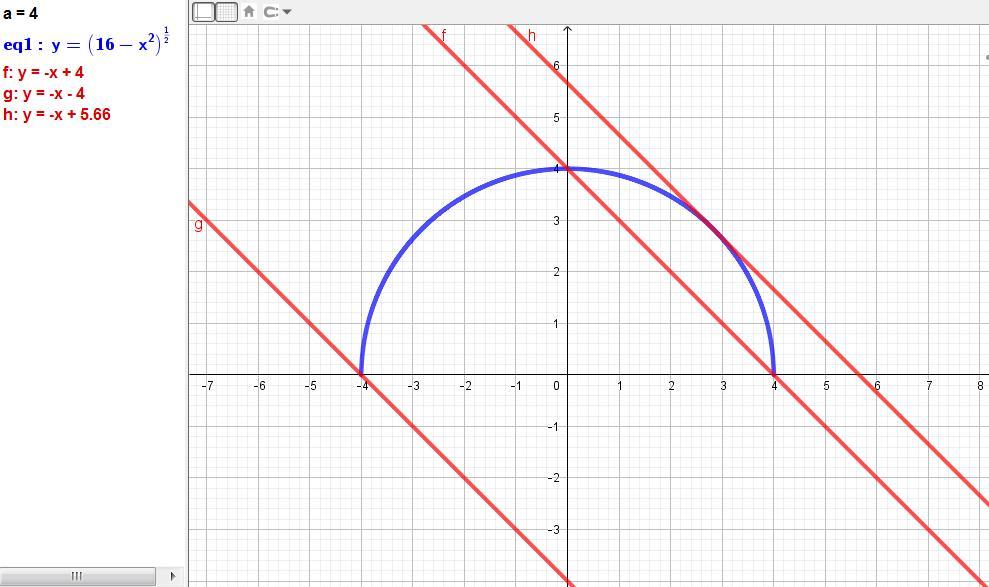
x^2 + t^2 = 4^2; t = a - x. Прямая должна пересекать полуокружность в одной точке.
x^2 + t^2 = 4^2; t = a - x. Прямая должна пересекать полуокружность в одной точке.
Через тригонометрию можно, но не так удобно
Ответы
Автор ответа:
2
Заданное уравнение х+√(16-х^2) = a представим так:
√(16-х^2) = -х + a.
Левая часть - уравнение полуокружности в положительной полуплоскости, правая - уравнение прямой, в котором параметр а соответствует ординате точки пересечения с осью Оу.
Возведём в квадрат.
16-х^2 = х²- 2aх + а².
Получили квадратное уравнение:
2х²- 2aх + (а² - 16) = 0.
Дискриминант D = 4a²- 4*2*(а² - 16) = -4а² + 128.
Уравнение имеет единственное решение, если дискриминант равен нулю:
-4а² + 128 = -4(а² - 32) = 0.
Отсюда а = +-4√2.
Но так как на промежутке а = (4...4√2) имеется 2 решения, а значение а = -4√2 выходит из области определения, то в ответ включаем:
-4 <= а < 4, а = 4√2.
Приложения:
спасибо большое
все верно
Похожие вопросы
Предмет: Русский язык,
автор: s8vet8lunobaСаmа
Предмет: Окружающий мир,
автор: hoper123
Предмет: Другие предметы,
автор: klimova09102002
Предмет: Физика,
автор: DIanaG20049
Предмет: История,
автор: ismailov2018