Question

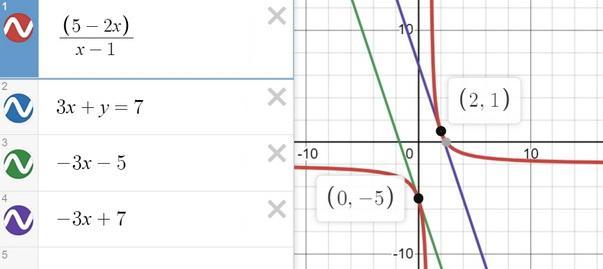
Найдите уравнение касательных графика функции y=5-2x/x-1 параллельных прямой 3x+y=7

Answer 1

Ответ:

Объяснение:

запишем прямую 3x+y=7  в виде у =kx +b, чтобы найти угловой коэффициент

у = -3х  +7

теперь мы знаем, что производная в точке касания будет равна -3

найдем эту точку

$\displaystyle y'=\bigg (\frac{5-2x}{x-1}\bigg )'=\frac{(5-2x)'(x-1)-(5-2x)(x-1)'}{(x-1)^2} =$

$\displaystyle =\frac{-2(x-1)-(5-2x)*1}{(x-1)^2} =\frac{-2x+2-5+2x}{(x-1)^2} =-\frac{3}{(x-1)^2}$

и мы знаем, что эта производная рана -3, поэтому мы можем найти х, что и будет координатой точки касания

$\displaystyle -\frac{3}{(x-1)^2} = -3 \\\\(x-1)^2 = 1\\\\x-1= \pm 1\\\\x_1 = 0\\x_2 = 2$

итак, мы нашли две точки касания

строим уравнение касательной в точке х₀ = 0

$\displaystyle y_k=y(x_0)+y'(x_0)(x-x_0)$

у нас все есть, кроме у(0) = -5

Yk = -5 +(-3)(x-0)

Yk = -5 -3x

теперь в точке х₀ = 2

y(2) = 1

Yk = 1+(-3)(x-2)

Yk = 1-3x +6

Yk = -3x +7  ---- а это и есть заданная прямая.

тогда наш ответ

уравнения касательных графика функции y=5-2x/x-1 параллельных прямой 3x+y=7

Yk₍₁₎ = -3х -5

Yk₍₂₎ = -3x +7