Предмет: Математика,
автор: Mrniwex
В прямоугольном треугольнике угол C равен 90*, угол A 30*, гипотенуза 2 . Найдите высоту CH
. Найдите высоту CH
bratabravl11:
гипотенуза 2✓3, а катет напротив 30° равен половине гипотенузе
то есть ✓3
Ответы
Автор ответа:
1
Ответ:
1.5
Пошаговое объяснение:
катет напротив угла в 30 градусов равен половине гипотенузы
БС=
по свойству высоты, проведенной из вершины прямого угла,
возводим в квадрат
возводим в квадрат
bh= x
Ты написал гипотенуза корень3, а в данных 2корень3
Автор ответа:
0
Ответ: CH=1,5 .
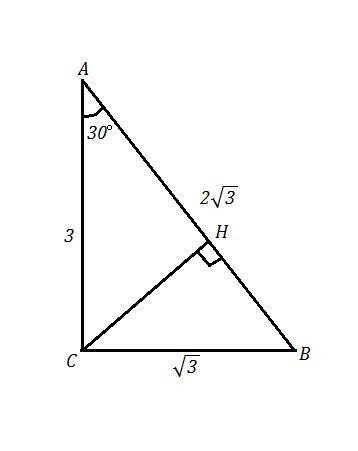
ΔАВС , ∠С=90° , ∠А=30° , АВ=2√3 , СН⊥АВ .
Против угла в 30° в прямоугольном треугольнике лежит катет ВС , равный половине гипотенузы ⇒ ВС=1/2*АВ=1/2*(2√3)=√3 .
По теореме Пифагора:
АС=√(АВ²-ВС²)=√(4·3-3)=√(12-3)=√9=3 .
Площадь треугольника:
S(ΔABC)=1/2*AC*BC=1/2*3*√3=(3√3)/2
S(ΔABC)=1/2*AB*CH ⇒ CH=2*S/AB = (3√3)/(2√3)=3/2=1,5
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: pushkinae
Предмет: Русский язык,
автор: Альберт20071
Предмет: Русский язык,
автор: миша294
Предмет: Алгебра,
автор: Обычная4554