Предмет: Алгебра,
автор: vityamath
Решить уравнение
a,b(пункты)
Приложения:
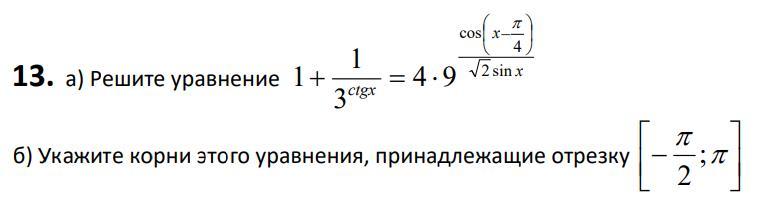
Ответы
Автор ответа:
2
Ответ:
Объяснение:
Похожие вопросы
Предмет: Русский язык,
автор: Aikko2016
Предмет: Английский язык,
автор: Аполинария16
Предмет: Қазақ тiлi,
автор: jadira83
Предмет: Математика,
автор: Аноним
Предмет: Математика,
автор: Lenysa35