Question

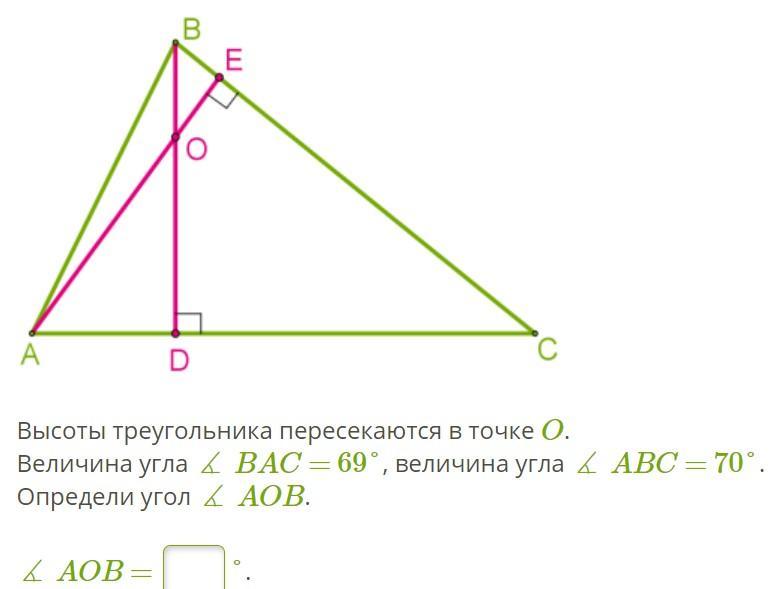
30 б. Высоты треугольника пересекаются в точке O.
Величина угла ∡ BAC = 69°, величина угла ∡ ABC = 70°.
Определи угол ∡ AOB.

∡ AOB = °.

Answer 1

Ответ:

∠AOB=139°

Объяснение:

сумма углов треугольника равна 180°

рассмотрим треугольник ABD угол ADB = 90° так как BD высота

угол BAD = BAC = 69°

найдем угол ABO = ABD

∠ABO = 180 - (∠ADB+BAD)

∠ABO = 180 - (90+69)

∠ABO = 21°

таким же способом находим ∠BAO = ∠BAE

∠AEB = 90° так как AE высота

∠ABE = ∠ABC = 70°

∠BAO = 180 - (∠AEB+∠ABE)

∠BAO = 180 - (90+70)

∠BAO = 20°

и наконец из треугольника ABO

найдем угол ∠AOB углы ∠BAO и ∠ABO нам теперь известны

∠AOB=180-(∠BAO+∠ABO)

∠AOB=180-(20+21)

∠AOB=139°