Предмет: Алгебра,
автор: aallllll
Помогите пожалуйста решить задачу
Приложения:
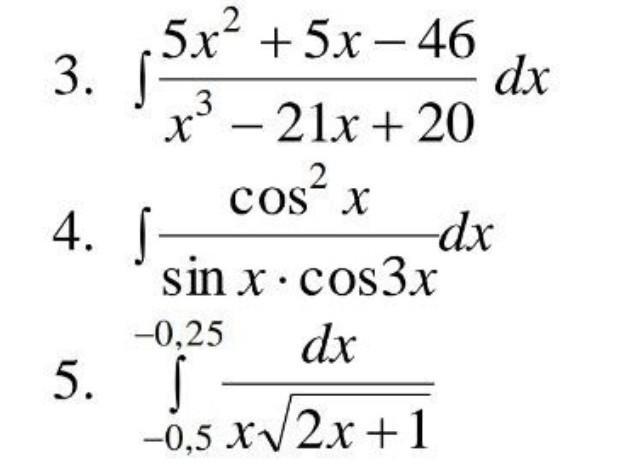
Ответы
Автор ответа:
1
Ответ:
Приложения:
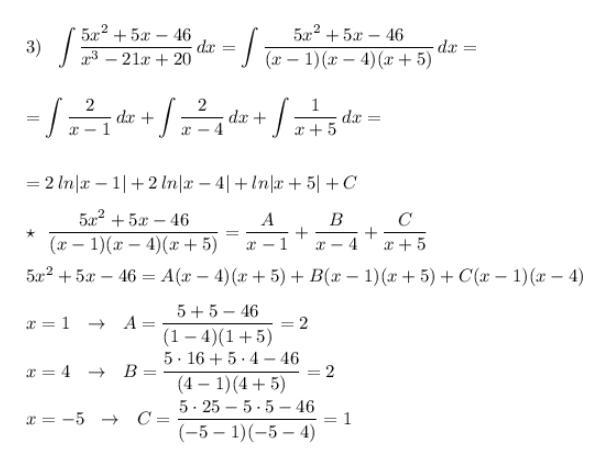
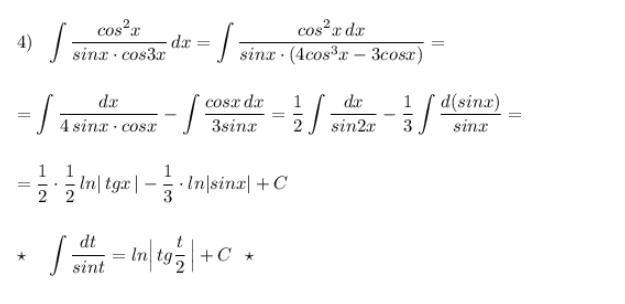
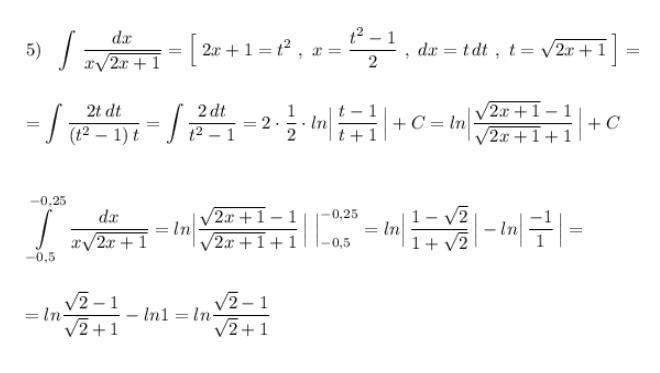
aallllll:
спасибо большое, добавьте скриншот пожалуйста
Похожие вопросы
Предмет: Английский язык,
автор: Vanyavano
Предмет: Русский язык,
автор: Eldosam0607
Предмет: Русский язык,
автор: полина562
Предмет: Русский язык,
автор: максимильян5
Предмет: Русский язык,
автор: иилария